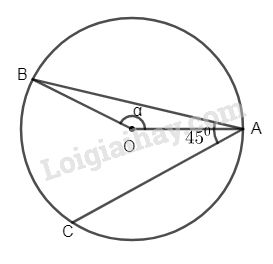
a) Đặt \(\widehat {AOB} = \alpha \Rightarrow {l_{\overparen{AB}}} =\dfrac {{\pi R\alpha } }{{180}}\)
\( \Rightarrow \dfrac{{5\pi R} }{ 6} = \dfrac{{\pi R\alpha }}{{180}} \Rightarrow \alpha = 150^\circ \).
b) Ta có \(sđ \overparen{ CB} = 90^o\)
\( \Rightarrow sđ \overparen{ AC} =360 - \left( {150 + 90} \right) = 120\)
Vậy \({l_{\overparen{AC}}} = \dfrac{{\pi R120} }{ {180}} = \dfrac{{2\pi R} }{3}\);
\({l_{\overparen{BC}}} = \dfrac{{\pi R90} }{ {180}} = \dfrac{{\pi R} }{ 2}\).