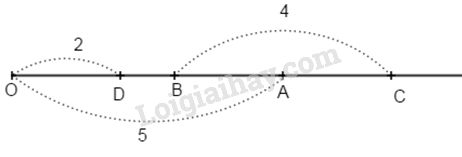
Vì A nằm giữa hai điểm B và C nên \(BA + AC = BC\) hay \(BA + AC = 4\) (cm) (1).
Mặt khác:
A và D cùng thuộc tia Ox mà \(OD < OA\; (2 < 5)\) nên D nằm giữa hai điểm O và A ta có :
\(OD + DA = OA\)
\(2 + DA = 5\)
\(DA = 5 - 2 = 3\) (cm).
Vì A nằm giữa hai điểm B và c nên BA và BC là hai tia trùng nhai và B nằm giữa hai điểm C và D nên BC và BD là hai tia đối nhau. Do đó BA và BD là hai tia đối nhau
=> B nằm giữa hai điểm A và D. Ta có \(BD + BA = AD\) hay \(BD + BA = 3\) (2).
Lấy (1) – (2) \(⇒ AC - BD = 1\) (3)
Theo đề ra \(AC = 2 BD\)
Ta có: \(2BD – BD = 1 ⇒ BD = 1\; cm\)
\(⇒ AC = 2.BD = 2.1 = 2\; (cm)\)