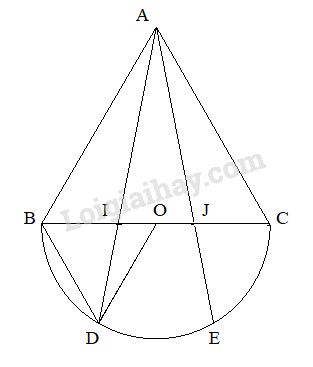
Ta có: \(\overparen{ BD} = \overparen{ DE} = \overparen{EC}\) (gt)
\(\Rightarrow sđ\overparen{BD} = sđ\overparen{DE} = sđ\overparen{ EC} =60^o\)
Do đó ∆BOD đều ( cân có một góc 60º)
\( \Rightarrow \widehat {OBD} = 60^\circ \)
Xét \(∆BID\) và \(∆CIA\) có :
\(\widehat {BID} = \widehat {CIA}\) ( đối đỉnh)
\(\widehat {OBD} = \widehat {ICA} = 60^\circ \)
Vậy ∆BID đồng dạng với ∆CIA (g.g)
\( \Rightarrow \dfrac{{BI} }{ {CI}} = \dfrac{{BD} }{ {CA}} =\dfrac {{OB} }{ {BC}} = \dfrac{1 }{ 2}\) ( vì \(BD = OB\) và \(CA = BC\))
\( \Rightarrow BI =\dfrac {1 }{ 3}BC\).
Tương tự, ta chứng minh được\(CJ =\dfrac {1 }{ 3}BC.\)
Do đó: \(BI = IJ = JC.\)