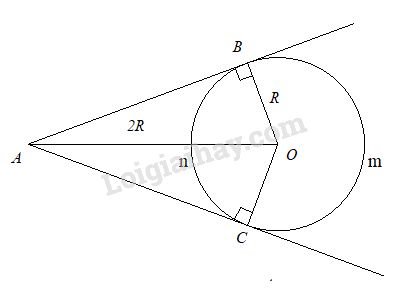
a) AB là tiếp tuyến của (O; R) nên AB \(\bot\) OB.
∆ABO vuông tại B có : OA = 2R, OB = R (gt) nên là nửa tam giác đều \(\Rightarrow \widehat {AOB} = 60^\circ \).
Do đó \(\widehat {BOC} = 2\widehat {AOB}\) (tính chất hai tiếp tuyến cắt nhau)
hay \(\widehat {BOC} = 120^\circ \).
b) Ta có: \(\widehat {BOC} = 120^\circ \) (cmt)
\(\Rightarrow sd\overparen{BnC}=120^o\)
\(\Rightarrow sd\overparen{BmC}=360^o-120^o=240^o\)