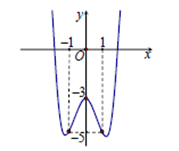
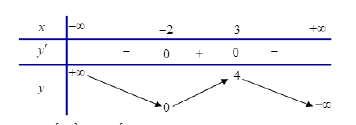
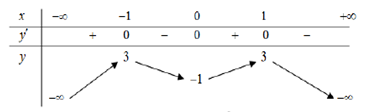
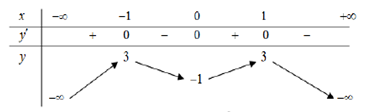
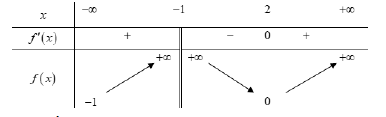
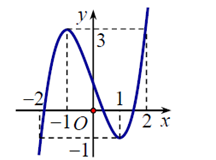
Đề kiểm tra 45 phút (1 tiết) - Đề số 3 - Chương I - Giải Tích 12
Lời giải
Bài Tập và lời giải
Bài 41.1 Trang 56 SBT hóa học 8
Căn cứ vào đồ thị về độ tan của chất rắn trong nước (hình 6.5, SGK), hãy ước lượng độ tan của các muối NaNO3, KBr, KNO3, NH4Cl, NaCl và Na2SO4 ở nhiệt độ :a) 20°C.b) 40°C.
Bài 41.2 Trang 56 SBT hóa học 8
Đề bài
Căn cứ vào đồ thị về độ tan của chất khí trong nước (hình 6.6, SGK), hãy ước lượng độ tan của các khí NO, O2 và N2 ở 20°C. Hãy cho biết có bao nhiêu mililít những khí trên tan trong 1 lít nước. Biết rằng ở 20°c và 1 atm, 1 mol chất khí có thể tích là 24 lít và khối lượng riêng của nước là 1 g/ml.
Bài 41.3 Trang 56 SBT hóa học 8
Tính khối lượng muối natri clorua NaCl có thể tan trong 750 g nước ở 25°C. Biết rằng ở nhiệt độ này độ tan của NaCl là 36,2 g.
Bài 41.4 Trang 56 SBT hóa học 8
Tính khối lượng muối AgNO3 có thể tan trong 250 g nước ở 25°C. Biết độ tan của AgNO3 ở 25°C là 222 g.
Bài 41.5* Trang 56 SBT hóa học 8
Đề bài
Biết độ tan của muối KCl ở 20°C là 34 g. Một dung dịch KCl nóng có chứa 50 g KCl trong 130 g H2O được làm lạnh về nhiệt độ 20°C. Hãy cho biết:
a) Có bao nhiêu gam KCl tan trong dung dịch.
b) Có bao nhiêu gam KCl tách ra khỏi dung dịch.
Bài 41.6 Trang 57 SBT hóa học 8
Một dung dịch có chứa 26,5 g NaCl trong 75 g H2O ở 25°C. Hãy xác định dung dịch NaCl nói trên là chưa bão hoà hay bão hoà.Biết độ tan của NaCl trong nước ở 25°C là 36 g.
Bài 41.7* Trang 57 SBT hóa học 8
Đề bài
Có bao nhiêu gam NaNO3 sẽ tách ra khỏi 200 g dung dịch bão hoà NaNO3 ở 50°C, nếu dung dịch này được làm lạnh đến 20°C?
Biết : \({S_{NaN{O_3}({{50}^o}C)}} = 114g;{S_{NaN{O_3}({{20}^o}C)}} = 88g\)