Hãy giải thích vì sao năng lượng truyền lên các bậc dinh dưỡng càng cao thì càng nhỏ dần

Đề bài

Diện tích hình chữ nhật thay đổi như thế nào nếu:

a) Chiều dài tăng \(3\) lần, chiều rộng không thay đổi?

b) Chiều rộng giảm \(2\) lần, chiều dài không thay đổi?

c) Chiều dài và chiều rộng đều tăng \(4\) lần?

d) Chiều dài tăng \(4\) lần, chiều rộng giảm \(3\) lần?

Đề bài

Cho hình chữ nhật có diện tích là \(20\) ( đơn vị diện tích) và hai kích thước là \(x\) và \(y\) (đơn vị dài)

a. Hãy điền vào ô trống trong bảng sau

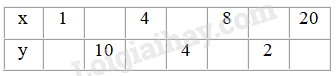
b) Theo bảng vừa thành lập, hãy biểu diễn bảy điểm của đồ thị hàm số \(y = \dfrac{{20}}{x}\) trên hệ trục tọa độ \(xOy.\)

Đề bài

a) Diện tích của hình chữ nhật tăng bao nhiêu phần trăm nếu mỗi cạnh tăng \(10\% ?\)

b) Diện tích của hình chữ nhật giảm bao nhiêu phần trăm nếu mỗi cạnh giảm \(10\% ?\)

Đề bài

Diện tích hình chữ nhật bằng 48 \(c{m^2}\)\(,\) một cạnh của nó có độ dài \(8cm.\) Đường thẳng song song với một trong các cạnh của hình chữ nhật chia hình chữ nhật đó thành hai hình chữ nhật bằng nhau. Tính chu vi của mỗi hình chữ nhật được tạo thành.

Đề bài

Tính các cạnh của một hình chữ nhật, biết rằng bình phương của độ dài một cạnh là \(16\) \((cm)\) và diện tích của hình chữ nhật là \(28\) \(c{m^2}\).

Đề bài

Tính các cạnh của một hình chữ nhật, biết tỉ số các cạnh là \(\dfrac{4}{9}\) và diện tích của nó là \(144.\)

Đề bài

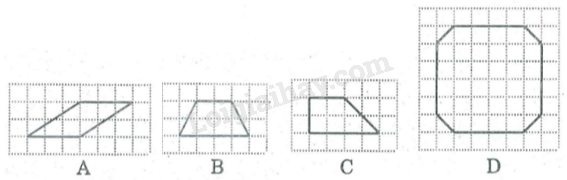
Tính diện tích các hình trên hình \(182\) (mỗi ô vuông là một đơn vị diện tích ).

Hãy giải thích vì sao được tính như vậy.

Đề bài

Trên giấy kẻ ô vuông, hãy vẽ:

a) Hai hình chữ nhật có cùng chu vi nhưng khác diện tích.

b) Hai hình chữ nhật có kích thước khác nhau nhưng cùng diện tích.

Đề bài

Cho hình bình hành \(ABCD\) \((h. 183).\) Từ \(A\) và \( C\) kẻ \(AH\) và \(CK\) vuông góc với đường chéo \(BD.\) Chứng minh rằng hai đa giác \(ABCH\) và \(ADCK\) có cùng diện tích.

Đề bài

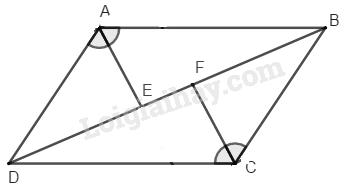
Cho hình bình hành \(ABCD\) \((h. 184).\) Đường phân giác của các góc \(A\) và \(C\) cắt đường chéo \(BD\) tại \(E, \,F.\)

a) Chứng minh rằng hai hình \(ABCFE\) và \(ADCFE\) có cùng diện tích.

b) Các hình đó có phải đa giác lồi không? Vì sao?

Đề bài

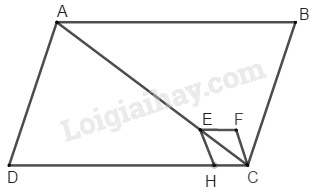
Trên hình \(185,\) các tứ giác \(ABCD\) và \(EFCH\) đều là hình bình hành. Điểm \(E\) nằm trên đường chéo \(AC.\)

a) Chứng minh rằng đa giác \(AEHD\) và hình \(ABCFE\) có cùng diện tích.

b) \(ABCFE\) có phải là đa giác lồi không? Vì sao?

Đề bài

Cho một tam giác vuông cân. Chứng minh rằng tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích của hình vuông dựng trên cạnh huyền (không sử dụng định lý Py-ta-go)

Đề bài

a) Nền của một phòng học có dạng hình chữ nhật, với chiều rộng đo được là \(4\,m\) và chiều dài là \(6\,m.\) Để có thể lát kín nền đó cần bao nhiêu viên gạch có hình vuông, với cạnh là \(33,33\,cm ?\)

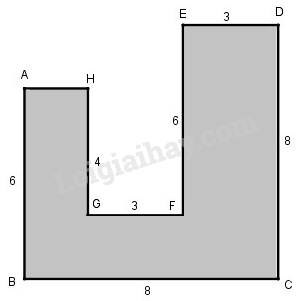
b) Cần bao nhiêu viên gạch có hình vuông, với cạnh là \(25\,cm\) để có thể lát kín một mảnh sân có dạng như hình bs.23 (biết \(AB = 6\,cm,\) \(BC = 8\,m,\) \(CD = 8\,m,\) \(DE = 3\,m,\) \(EF = 6\,m,\) \(FG = 3\,m,\) \(GH = 4\,m\) và góc tại các đỉnh \(A, B, C, D, E, F, G, H\) đều là góc vuông)?

Đề bài

a) Dùng diện tích để chứng tỏ : \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\)

b) Dùng diện tích để chứng tỏ : \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\)với điều kiện \(b < a\)

Đề bài

Đố vui

a) Có thể dùng kéo cắt một lần và chỉ cắt theo đường thẳng, chia một hình chữ nhật thành hai mảnh để ghép lại được một tam giác vuông hay không ?

b) Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thằng, chai một hình chữ nhật thành ba mảnh để ghép lại được một tam giác thường hay không ?