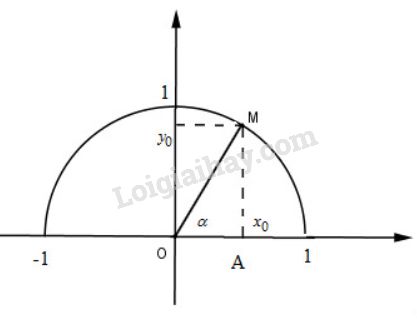
+) Định nghĩa: Với mỗi góc \(α\) \((0^0≤ α ≤ 180^0)\) ta xác định một điểm \(M\) trên nửa đường tròn đơn
vị sao cho góc \(xOM = α\) và giả sử điểm \(M\) có tọa độ \(M (x_0;y_0)\).
Khi đó ta có định nghĩa:
Sin của góc \(α\) là \(y_0\), kí hiệu là \(\sin α = y_0\)
cosin của góc \(α\) là \(x_0\), kí hiệu là \(\cos α = x_0\)
tang của góc \(α\) là \(( x_0≠ 0)\), ký hiệu \(\tan α = {{{y_0}} \over {{x_0}}}\)
cotang cuả góc \(α\) là \((y_0≠ 0)\), ký hiệu \(\cot α = {{{x_0}} \over {{y_0}}}\)
Các số \(\sin α, \cos α, \tan α, \cot α\) được gọi là các giá trị lượng giác của góc \( α\).
+) Khi \(α\) là các góc nhọn thì:
+ Theo định nghĩa ta có: \(\sin α = y_0\)
Trong tam giác \(OAM\) vuông tại \(A\), ta có: \(\sin \alpha = {{{y_0}} \over 1} = {y_0}\)
+ Theo định nghĩa ta có: \(\cos α = x_0\)
Trong tam giác \(OAM\) vuông tại \(A\), ta có: \(\cos \alpha = {{OA} \over {OM}} = {{{x_0}} \over 1} = {x_0}\)
+ Theo định nghĩa ta có: \(\tan \alpha = {{{y_0}} \over {{x_0}}}({x_0} \ne 0)\)
Trong tam giác \(OAM\) vuông tại \(A\), ta có: \(\tan \alpha = {{AM} \over {OA}} = {{{y_0}} \over {{x_0}}}\)
+ Theo định nghĩa ta có: \(\cot \alpha = {{{x_0}} \over {{y_0}}}({y_0} \ne 0)\)
Trong tam giác \(OAM\) vuông tại \(A\), ta có: \(\cot \alpha = {{OA} \over {AM}} = {{{x_0}} \over {{y_0}}}\)