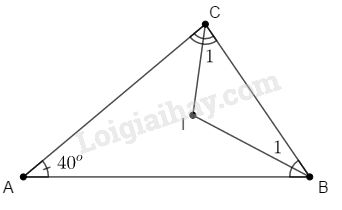
Áp dụng định lí tổng các góc của một tam giác vào \(\Delta ABC\) ta có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat B + \widehat C = {180^o} - \widehat A\\ \Rightarrow \widehat B + \widehat C = {180^o} - {40^o} = {140^o}\end{array}\)
\(\widehat {{B_1}} = \dfrac{1}{2}\widehat B\) (vì \(BI\) là tia phân giác góc \(B\)).
\(\widehat {{C_1}} = \dfrac{1}{2}\widehat C\) (vì \(CI\) là tia phân giác góc \(C\)).
Áp dụng định lí tổng các góc của một tam giác vào \(\Delta BIC\) ta có:
\(\begin{array}{l}\widehat {{B_1}} + \widehat {{C_1}} + \widehat {BIC} = {180^o}\\ \Rightarrow \widehat {BIC} = {180^o} - \left( {\widehat {{B_1}} + \widehat {{C_1}}} \right)\\ \Rightarrow \widehat {BIC} = {180^o} - \dfrac{1}{2}\left( {\widehat B + \widehat C} \right)\\ \Rightarrow \widehat {BIC} = {180^o} - \dfrac{1}{2}{.140^o} = {110^o}\end{array}\)
Chọn C.
Bài 1.2
Tam giác \(ABC\) có \(\widehat A = {75^o}\). Tính \(\widehat B\) và \(\widehat C\), biết :
a) \(\widehat B = 2\widehat C\);
b) \(\widehat B - \widehat C = {25^o}\).
Phương pháp:
Định lí: Tổng ba góc của một tam giác bằng \({180^0}\).
Áp dụng định lí tổng các góc của một tam giác vào \(\Delta ABC\), ta có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat B + \widehat C = {180^o} - \widehat A\\ \Rightarrow \widehat B + \widehat C = {180^o} - {75^o} = {105^o}\,\,\,\,(1)\end{array}\)
a) Thay \(\widehat B = 2\widehat C\) vào (1) ta được:
\(\begin{array}{l}2\widehat C + \widehat C = {105^o}\\ \Rightarrow 3\widehat C = {105^o}\\ \Rightarrow \widehat C = {105^o}:3 = {35^o}\\ \Rightarrow \widehat B = 2\widehat C = {2.35^o} = {70^o}\end{array}\)
b) \(\widehat B - \widehat C = {25^o} \Rightarrow \widehat B = \widehat C + {25^o}\,\,\,(2)\)
Thay (2) vào (1) ta được:
\(\begin{array}{l}\widehat C + {25^o} + \widehat C = {105^o}\\ \Rightarrow 2\widehat C + {25^o} = {105^o}\\ \Rightarrow 2\widehat C = {105^o} - {25^o}\\ \Rightarrow 2\widehat C = {80^o}\\ \Rightarrow \widehat C = {80^o}:2 = {40^o}\\ \Rightarrow \widehat B = \widehat C + {25^o} = {40^o} + {25^o} = {65^o}\end{array}\)
Bài 1.3
Tam giác \(ABC\) có \(\widehat B = {110^o},\widehat C = {30^o}\). Gọi \(Ax\) là tia đối của tia \(AC.\) Tia phân giác của góc \(BAx\) cắt đường thẳng \(BC\) tại \(K.\) Chứng minh rằng tam giác \(KAB\) có hai góc bằng nhau.
Phương pháp:
- Góc ngoài tam giác bằng tổng hai góc trong không kề với nó.
- Tổng số đo hai góc kề bù bằng \(180^o\).
\(\widehat {ABK} = {180^o} - {110^o} = {70^o}\) (hai góc kề bù) (1)
\(\widehat {BAx} = {110^o} + {30^o} = {140^o}\) (tính chất góc ngoài tam giác)
\(\widehat {BAK} = \dfrac{1}{2}\widehat {BAx} = \dfrac{1}{2}{.140^o} = {70^o}\) (vì \(AK\) là tia phân giác góc \(A\)) (2)
Từ (1) và (2) suy ra tam giác \(KAB\) có hai góc bằng nhau.
Bài 1.4
Cho tam giác \(ABC\) vuông tại \(A.\) Gọi \(d\) là đường thẳng vuông góc với \(BC\) tại \(C.\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D\) và cắt \(d\) ở \(E.\) Chứng minh rằng tam giác \(CDE\) có hai góc bằng nhau.
Phương pháp:
- Trong tam giác vuông hai góc nhọn phụ nhau.
- Hai góc đối đỉnh thì bằng nhau.
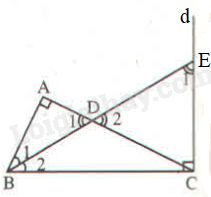
\(\widehat {{D_1}} = \widehat {{D_2}}\) (hai góc đối đỉnh).
\(\widehat {{D_1}} + \widehat {{B_1}} = {90^o}\) (trong tam giác vuông hai góc nhọn phụ nhau).
\( \Rightarrow \widehat {{D_2}} + \widehat {{B_1}} = {90^o}\) (*)
\(\widehat {{B_2}} + \widehat {{E_1}} = {90^o}\) (trong tam giác vuông hai góc nhọn phụ nhau).
Mặt khác \(\widehat {{B_1}} = \widehat {{B_2}}\) (vì \(BE\) là phân giác góc \(B\)).
\( \Rightarrow \widehat {{B_1}} + \widehat {{E_1}} = {90^o}\) (2*)