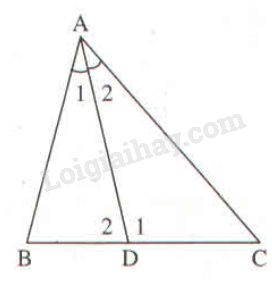
Xét \(∆ABD\) ta có \(\widehat {{D_1}}\) là góc ngoài tại đỉnh \(D.\)
\(\widehat {{D_1}} = \widehat B + \widehat {{A_1}}\) (tính chất góc ngoài của tam giác)
Xét \(∆ADC\) ta có \(\widehat {{D_2}}\) là góc ngoài tại đỉnh \(D.\)
\(\widehat {{D_2}} = \widehat C + \widehat {{A_2}}\) (tính chất góc ngoài của tam giác)
Ta có: \(\widehat B - \widehat C = 20^\circ \left( {gt} \right);\) \(\widehat {{A_1}} = \widehat {{A_2}}\left( {gt} \right)\)
\( \Rightarrow \widehat {{D_1}} - \widehat {{D_2}} = \left( {\widehat B + \widehat {{A_1}}} \right) \)\(\,- \left( {\widehat C + \widehat {{A_2}}} \right)\)
\( = \widehat B - \widehat C = 20^\circ \)
\(\widehat {{D_1}} + \widehat {{D_2}} = 180^\circ \) (hai góc kề bù)
\(\eqalign{
& \Rightarrow \widehat {{D_1}} = \left( {180^\circ + 20^\circ } \right):2 = 100^\circ \cr
& \Rightarrow \widehat {{D_2}} = 180^\circ - 100^\circ = 80^\circ \cr} \)
Vậy \(\widehat {A{\rm{D}}C} = 100^\circ ;\widehat {A{\rm{D}}B} = 80^\circ \).