Phương pháp:
+ Trong tam giác tù, góc tù là góc lớn nhất và cạnh đối diện với góc tù là cạnh lớn nhất.
+ Trong một tam giác, đối diện với cạnh lớn hơn là góc lớn hơn.
Do \(Â\) là góc tù nên \(Â\) là góc lớn nhất.
Vậy trong tam giác \(ABC\) có \(\widehat A > \widehat B > \widehat C.\) Từ đó suy ra \(BC > AC > AB\) (đối diện với góc lớn hơn là cạnh lớn hơn)
Chọn (D).
Bài 1.2
Tam giác \(ABC\) có \(AB = 5cm, BC = 6cm và AC = 7cm.\) Gọi \({\widehat A_1},\widehat {{B_1}},\widehat {{C_1}}\) theo thứ tự là góc ngoài tại đỉnh \(A, B, C\) của tam giác đó. Trong các khẳng định sau, khẳng định nào đúng?
\(\left( A \right)\widehat {{A_1}} > \widehat {{B_1}} > \widehat {{C_1}}\)
\(\left( B \right)\widehat {{B_1}} > \widehat {{C_1}} > \widehat {{A_1}}\)
\(\left( C \right)\widehat {{C_1}} > \widehat {{A_1}} > \widehat {{B_1}}\)
\(\left( D \right)\widehat {{C_1}} > \widehat {{B_1}} > \widehat {{A_1}}\)
Phương pháp:
Sử dụng:
+ Hai góc kề bù có tổng số đo bằng \(180^0.\)
+ Trong một tam giác, đối diện với cạnh lớn hơn là góc lớn hơn.
Cách giải:
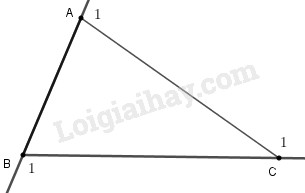
Theo tính chất hai góc kề bù, ta có \(\widehat {{A_1}} = 180^\circ - \widehat A;\widehat {{B_1}} = 180^\circ - \widehat B;\)\(\widehat {{C_1}} = 180^\circ - \widehat C\)
Theo giả thiết, trong tam giác \(ABC\) ta có \(AB < BC < AC.\)
Từ đó suy ra \(\widehat C < \widehat A < \widehat B\) (đối diện với cạnh lớn hơn là góc lớn hơn)
Suy ra: \( 180^\circ - \widehat C> 180^\circ - \widehat A> 180^\circ - \widehat B\)
Hay \(\widehat {{C_1}} > \widehat {{A_1}} > \widehat {{B_1}}\).
Chọn \(\left( C \right)\)
Bài 1.3
So sánh các cạnh của một tam giác cân, biết rằng nó có một góc ngoài bằng \(40°.\)
Phương pháp:
Sử dụng:
+ Hai góc kề bù có tổng số đo bằng \(180^0\)
+ Trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.
Cách giải
Theo giả thiết, tam giác cân này có một góc ngoài bằng \(40°\) nên nó có một góc trong bằng \(180° - 40° = 140°.\) Góc trong này không thể là góc ở đáy của tam giác cân mà phải là góc ở đỉnh và góc này là góc lớn nhất của tam giác. Vậy cạnh đáy của tam giác cân là cạnh lớn nhất và lớn hơn hai cạnh bên của nó.