Phương pháp:
Sử dụng:
+) Trong một tam giác, góc ngoài tại một đỉnh lớn hơn góc trong tại đỉnh không kề với đỉnh đó.
+) Trong tam giác tù, đối diện với góc tù là cạnh lớn nhất.
+) Trong một tam giác, đối diện với góc lớn hơn là cạnh lớn hơn.
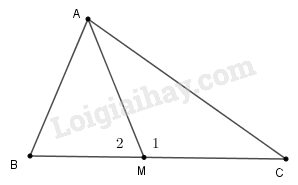
Ta có \(\widehat {{M_1}} + \widehat {{M_2}} = 180^\circ \) nên chỉ có hai khả năng xảy ra ứng với các vị trí của \( M\) trên \( BC\) là \(\widehat {{M_1}} > 90^\circ \) hoặc \(\widehat {{M_2}} \ge 90^\circ \).
- Nếu \(\widehat {{M_1}} > 90^\circ \) thì tam giác \( AMC\) có góc \(\widehat {AMC}\) tù nên \( AM > AC\)
- Nếu \(\widehat {{M_2}} \ge 90^\circ \) thì trong tam giác \(ABM\) có \(AM < AB.\) Kết hợp với giả thiết \(AB \leqslant AC,\) ta suy ra \( AM < AC.\)
Vậy ta luôn có \( AM < AC.\)
Bài 1.5
Cho tam giác \(ABC\) với \(AB ≤ BC ≤ CA.\) Trên các cạnh \(BC\) và \(AC\) lần lượt lấy hai điểm \(M\) và \(N\) (khác \(A, B, C\)). Chứng minh rằng \(MN < AC.\)
Phương pháp:
Sử dụng kết quả bài 1.4
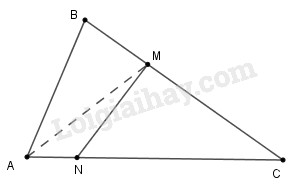
Kẻ đoạn thẳng \(AM.\)
Xét tam giác \(MAC.\) Chứng minh tương tự như bài 1.4 ta có \(MN < a,\) trong đó \(a\) là đoạn lớn nhất trong hai đoạn thẳng \(MA\) và \(MC.\)
Trong tam giác \(ABC\) có \(AB ≤ AC, M ∈ BC\) \((M \ne B, M \ne C);\)
Chứng minh tương tự bài 1.4, ta có \(AM < AC.\)
Mặt khác \(MC < BC ≤ CA.\)
Suy ra: \(MA<AC;MC<AC\)
Từ đó: \(a < AC,\) do đó \(MN < AC.\)
Bài 1.6
Cho tam giác \(ABC\) có góc \(A\) tù. Trên cạnh \(AB\) lấy điểm \(D\) (khác \(A\) và \(B),\) trên cạnh \(AC\) lấy điểm \(E\) (khác \(A\) và \(C).\) Chứng minh rằng \(DE < BC.\)
Phương pháp:
Sử dụng:
+) Trong một tam giác, góc ngoài tại một đỉnh lớn hơn góc trong tại đỉnh không kề với đỉnh đó.
+) Trong tam giác tù, góc tù là góc lớn nhất và đối diện với góc tù là cạnh lớn nhất.
+) Trong một tam giác, đối diện với góc lớn hơn là cạnh lớn hơn.
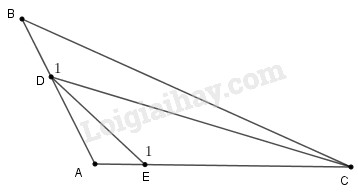
Xét tam giác \(CDE.\)
Ta có \(\widehat {E_1} > \widehat A\) (góc ngoài tại đỉnh \(E\) của tam giác \(ADE)\), mà \(Â \) là góc tù nên \(\widehat {{E_1}}\) là góc tù.
Xét tam giác \(EDC\) có \(\widehat {{E_1}}\) là góc tù nên \(\widehat {{E_1}}>\widehat {ECD}\)
Suy ra \(CD > DE \) (1) (đối diện với góc lớn hơn là cạnh lớn hơn)
Xét tam giác \(BCD.\)
Ta có \(\widehat {{D_1}} > \widehat A\) (góc ngoài tại đỉnh \(D\) của tam giác \(ADC)\), mà \(Â \) là góc tù nên \(\widehat {{D_1}}\) là góc tù.
Xét tam giác \(BDC\) có \(\widehat {{D_1}}\) là góc tù nên \(\widehat {{D_1}}>\widehat {CBD}\)
Suy ra \(BC > CD \) (2) (đối diện với góc lớn hơn là cạnh lớn hơn)
Từ (1) và (2) suy ra \(BC > DE.\)