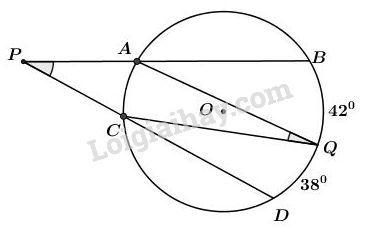
Ta có \(\widehat {BP{\rm{D}}}\) là góc ở ngoài đường tròn (O) nên:
\(\displaystyle \widehat {BPD} = {sđ\overparen{BQD} -sđ\overparen{AC}\over 2}\) (góc có đỉnh nẳm ngoài đường tròn chắn cung \(AC\) và \(BD\)).
Ta có \(\widehat {AQC}\) là góc nội tiếp trong đường tròn (O) nên:
\(\displaystyle \widehat {AQC} = {1 \over 2}sđ\overparen{AC}\) (góc nội tiếp chắn cung \(AC\)).
\(\displaystyle \Rightarrow \widehat {BPD} + \widehat {AQC} = {sđ\overparen{BQD} -sđ\overparen{AC} \over 2} + {1 \over 2}sđ\overparen{AC}\)
\(\displaystyle ={1 \over 2}sđ\overparen{BQD}={{{{42}^0} + {{38}^0}} \over 2} = {40^0}.\)
Vậy \(\widehat {BP{\rm{D}}} + \widehat {AQC} = {40^0}.\)