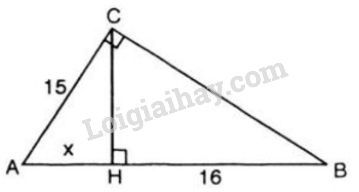
Đặt \(AH = x\) \((x > 0).\)
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\) có đường cao \(AH\) ta có: \(AC^2 = AB.AH\)
\(\begin{array}{l} \Leftrightarrow {15^2} = \left( {x + 16} \right)x\\ \Leftrightarrow {x^2} + 16x - 225 = 0\\ \Leftrightarrow \left( {x - 9} \right)\left( {x + 25} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 9 = 0\\x + 25 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 9\;\;\left( {tm} \right)\\x = - 25\;\;\left( {ktm} \right)\end{array} \right..\\ \Rightarrow AH = 9\;cm.\end{array}\)
Ta có: \(HC^2 = AH. HB = 9. 16 = 144\)
\(\Rightarrow\)\(HC=12\) \((cm).\)
Vậy diện tích tam giác \(ABC\) là:
\(\displaystyle S = {1 \over 2}AB.CH = {1 \over 2}.(16+9).12 = 150(c{m^2}).\)