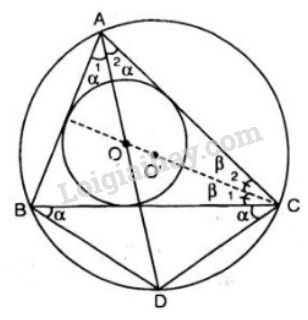
Vì \(AC\) và \(BC\) tiếp xúc với đường tròn \((O)\), \(AD\) đi qua \(O\) nên ta có:
\(\widehat {CA{\rm{D}}} = \widehat {BA{\rm{D}}} = \alpha\) (vì tâm đường tròn nội tiếp trong tam giác là giao điểm của ba đường phân giác trong tam giác)
\(⇒\) \(\overparen{CD}=\overparen{DB}\) \(⇒CD = DB\) (*)
Tương tự, \(CO\) là tia phân giác của góc \(C\) nên:
\(\widehat {AC{\rm{O}}} = \widehat {BCO} = \beta .\)
Mặt khác: \(\widehat {DCO} = \widehat {DCB} + \widehat {BCO} = \alpha + \beta \, \,(1)\) (do \(\widehat {BA{\rm{D}}} = \widehat {BC{\rm{D}}}\))
Ta có: \(\widehat {CO{\rm{D}}}\) là góc ngoài của \(∆ AOC\) nên
\(\widehat {CO{\rm{D}}} = \widehat {OAC} + \widehat {OC{\rm{A}}} = \beta + \alpha \, \, (2)\)
Từ (1) và (2) ta có: \(\widehat {OC{\rm{D}}} = \widehat {CO{\rm{D}}}\)
Vậy \(∆DOC\) cân tại \(D\) (2*)
Từ (*) và (2*) suy ra \(CD = OD = BD.\)
Chọn đáp án \(D\).