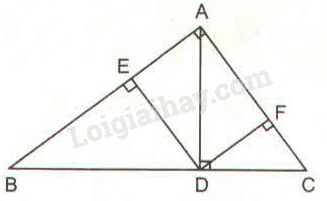
Vì \(DE\) và \(CA\) cùng vuông góc với \(AB\) nên \(DE // AC\).
Xét \(\Delta ABC\) có \(DE//AC\)
Theo định lí Ta-lét, ta có:
\(\displaystyle {{AE} \over {AB}} = {{CD} \over {CB}}\) (1)
Vì \(DF\) và \(BA\) cùng vuông góc với \(AC\) nên \(DF//AB\).
Xét \(\Delta ABC\) có \(DF//AB\)
Theo định lí Ta-lét, ta có:
\(\displaystyle {{AF} \over {AC}} = {{BD} \over {BC}}\) (2)
Cộng (1) và (2) theo vế với vế, ta có:
\(\displaystyle {{AE} \over {AB}} + {{AF} \over {AC}} = {{CD} \over {CB}} + {{BD} \over {BC}}\)
\(\displaystyle \Rightarrow {{AE} \over {AB}} + {{AF} \over {AC}}= {{CD + BD} \over {BC}}\)
\(\displaystyle \Rightarrow {{AE} \over {AB}} + {{AF} \over {AC}} = {{BC} \over {BC}} = 1\)
Tổng \(\displaystyle {{AE} \over {AB}} + {{AF} \over {AC}}\) không thay đổi vì luôn có giá trị bằng \(1.\)
Vậy khi độ dài cạnh góc vuông \(AB, AC\) của tam giác vuông \(ABC\) thay đổi thì tổng \(\displaystyle {{AE} \over {AB}} + {{AF} \over {AC}}\) luôn luôn không thay đổi. Tổng đó luôn có giá trị bằng \(1.\)