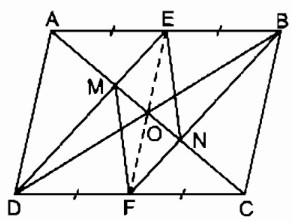
a. Xét tứ giác DEBF: AB // CD (gt) hay DF // EB
EB = \(\displaystyle {1 \over 2}\)AB (gt)
DF = \(\displaystyle {1 \over 2}\)CD (gt)
Suy ra: EB = DF
Tứ giác DEBF là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
b. Gọi O là giao điểm của AC và BD
OB = OD (tính chất hình bình hành)
Tứ giác DEBF là hình bình hành
nên EF và BD cắt nhau tại trung điểm của mỗi đường
Suy ra: EF đi qua trung điểm O của BD
Vậy AC, BD và EF cắt nhau tại O trung điểm của mỗi đoạn
c. Xét ∆ EOM và ∆ FON:
\(\widehat {MEO} = \widehat {NFO}\) (so le trong)
OE = OF (tính chất hình bình hành)
\(\widehat {MOE} = \widehat {NOF}\) (đối đỉnh)
Do đó : ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường )