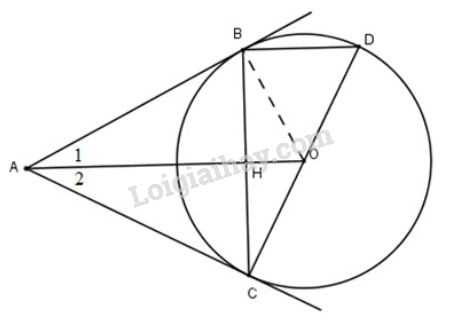
a) Vì \(AB,\ AC\) là các tiếp tuyến nên \(AB=AC\) và \(\widehat{A_{1}}=\widehat{A_{2}}\) (Tính chất hai tiếp tuyến cắt nhau)
Suy ra \(\Delta{ABC}\) cân tại \(A\).
Vì \(\widehat{A_{1}}=\widehat{A_{2}}\) nên \(AO\) là tia phân giác của góc \(A\) nên \(AO\) đồng thời là đường cao ứng với cạnh \(BC\).
vậy \(OA\perp BC\)
b) Điểm \(B\) nằm trên đường tròn đường kính \(CD\) nên \(\widehat{CBD}=90^{\circ}\) hay \(BC \bot BD\).
Lại có \(AO \bot BC\)
Suy ra \(BD // AO\) (vì cùng vuông góc với \(BC)\).
c) Nối \(OB\) thì \(OB \perp AB.\)
Xét tam giác \(AOB\) vuông tại \(B\), ta có:
\(\sin \widehat {{A_1}} = \dfrac{OB}{OA}=\dfrac{2}{4}=\dfrac{1}{2}\)
\(\Rightarrow \widehat{A_{1}}=30^{\circ}\Rightarrow \widehat{BAC}=60^{\circ}.\)
Tam giác \(ABC\) cân, có một góc \(60^{\circ}\) nên là tam giác đều.
Suy ra \(AB=BC=CA\)
Xét tam giác \(AOB\) vuông tại \(B\), áp dụng định lí Pytago, ta có:
\(AO^{2}=AB^{2}+OB^{2} \Rightarrow AB^2=AO^2-OB^2\)
\(\Leftrightarrow AB^2=4^{2}-2^{2}=16-4=12 \Rightarrow AB=2\sqrt{3.}\)
Vậy \(AB=AC=BC=2\sqrt{3}cm\).
Nhận xét. Qua câu c) ta thấy: Góc tạo bởi hai tiếp tuyến của một đường tròn vẽ từ một điểm cách tâm một khoảng bằng đường kính đúng bằng \(60^{\circ}\).