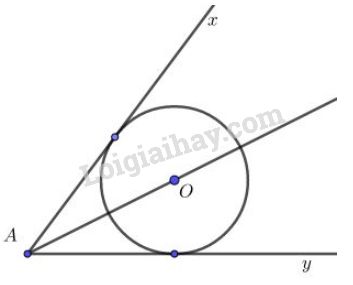
Gọi \(O\) là tâm của một đường tròn bất kì tiếp xúc với hai cạnh góc \(xAy\). Khi đó \(Ax,\ Ay\) là hai tiếp tuyến của đường tròn \((O)\). Theo tính chất của hai tiếp tuyến cắt nhau ta có:
\(\widehat {xAO} = \widehat {y{\rm{A}}O}\)
Hay \(AO\) là tia phân giác của góc \(xAy\). Vậy tập hợp tâm các đường tròn tiếp xúc với hai cạnh của góc \(xAy\) nằm trên tia phân giác của góc \(\widehat{xAy}\).