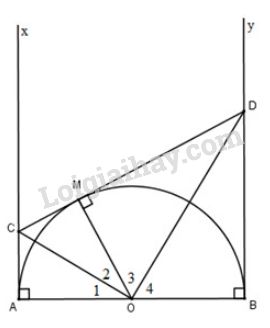
Ta có:
\(OA\perp AC\)
\(OB\perp BD\)
Suy ra \(Ax,\ By\) là các tiếp tuyến của đường tròn lần lượt tại \(A,\ B\).
Vì \(CA,\ CM\) là hai tiếp tuyến của \((O)\) lần lượt tại \(A\) và \(M\), theo tính chất hai tiếp tuyến cắt nhau, ta có: \(CM =CA\) và \(\widehat{O_1}=\widehat{O_2}\)
Lập luận tương tự, ta cũng có: \(DM=DB\) và \(\widehat{O_3}=\widehat{O_4}\)
a) Ta có:
\(\eqalign{
& \widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} + \widehat {{O_4}} = {180^o} \cr
& \Leftrightarrow \widehat {{O_2}} + \widehat {{O_2}} + \widehat {{O_3}} + \widehat {{O_3}} = {180^o} \cr
& \Leftrightarrow \left( {\widehat {{O_2}} + \widehat {{O_2}}} \right) + \left( {\widehat {{O_3}} + \widehat {{O_3}}} \right) = {180^o} \cr
& \Leftrightarrow 2\widehat {{O_2}} + 2\widehat {{O_3}} = {180^o} \cr
& \Leftrightarrow 2\left( {\widehat {{O_2}} + \widehat {{O_3}}} \right) = {180^o} \cr
& \Leftrightarrow \widehat {{O_2}} + \widehat {{O_3}} = {90^o} \cr
& \Leftrightarrow \widehat {COD} = {90^o} \cr} \)
b) Ta có: \(CM=AC,\ MD=BD\) (chứng minh trên)
Lại có: \(CD=CM+MD=AC+BD\)
c) Xét tam giác \(COD\) vuông tại \(O\), áp dụng hệ thức lượng trong tam giác vuông, ta có:
\(MO^2=MC.MD=AC.BD=R^2\)
Vì bán kính đường tròn không đổi khi \(M\) di chuyển trên nửa đường tròn nên \(MO^2\) không đổi do đó tích \(AC.BD\) không đổi khi \(M\) di chuyển trên nửa đường tròn.