Gọi \(x (cm)\) là độ dài một cạnh của hình chữ nhật thì cạnh kia có độ dài \(20 – x (cm)\).
Điều kiện: \(0<x<20\)
Diện tích hình chữ nhật là \(S\left( x \right) = x\left( {20 - x} \right) = 20x - {x^2}\) với \(x \in \left( {0;20} \right)\)
Ta có \(S'\left( x \right) = 20 - 2x;S'\left( x \right) = 0 \Leftrightarrow x = 10\)
\(S\left( {10} \right) = 100\)
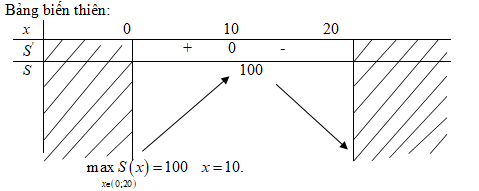
Vậy hình chữ nhật có diện tích lớn nhất khi nó là hình vuông có cạnh dài \(10 cm\).