a) Hàm số \(y = -2x + 3.\)
Cho \(x=0 \Rightarrow y=-2.0+3=0+3=3 \Rightarrow A(0; 3)\)
Cho \(y=0 \Rightarrow 0=-2.x+3 \Leftrightarrow x=\dfrac{3}{2} \Rightarrow B{\left(\dfrac{3}{2}; 0\right)}\)
Vẽ đường thẳng đi qua hai điểm \(A(0; 3)\) và \(B{\left(\dfrac{3}{2}; 0\right)}\) ta được đồ thị hàm số \(y = -2x + 3.\).
Đồ thị được vẽ như hình bên.
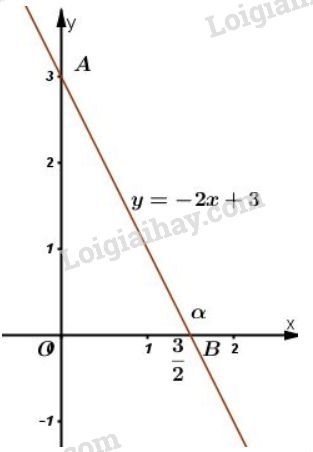
b) Gọi \(\alpha \) là góc giữa đường thẳng \(y = -2x + 3\) và trục \(Ox \Rightarrow \alpha = \widehat{ABx}\).
Xét tam giác vuông \(OAB\) vuông tại \(O\), ta có:
\(\tan \widehat {OBA} = \dfrac{OA}{OB} = \dfrac{3}{\dfrac{3}{2}}=2\)
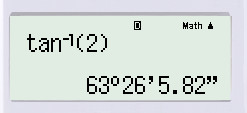
Thực hiện bấm máy tính, ta được:
\(\widehat {ABO} \approx {63^0}26'\)
Lại có \(\widehat {ABO}\) và \(\widehat {ABx}\) là hai góc kề bù, tức là:
\(\widehat {ABO} + \widehat {ABx} =180^0\)
\(\Leftrightarrow \widehat {ABx}=180^0 -\widehat {ABO} \)
\(\Leftrightarrow \widehat {ABx} \approx 180^0 -{63^0}26' \)
\(\Leftrightarrow \widehat {ABx} \approx 116^0 34'\)
Vậy \(\alpha \approx {116^0}34'\).