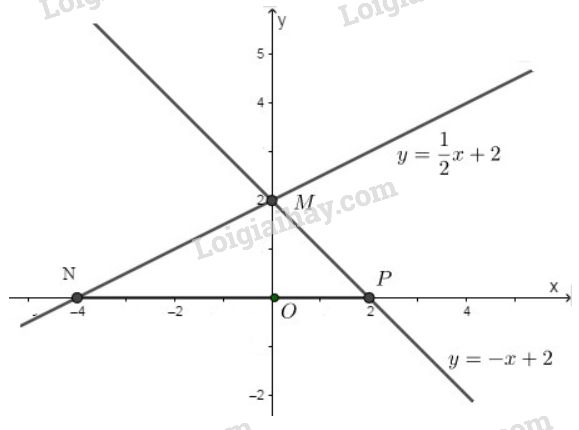
a) Đồ thị được vẽ như hình dưới:
+) Hàm số \(y = \dfrac{1}{2}x + 2\):
Cho \(x=0 \Rightarrow y=\dfrac{1}{2}.0 + 2=0+2=2 \Rightarrow M(0; 2)\).
Cho \(y=0 \Rightarrow 0=\dfrac{1}{2}.x + 2 \Rightarrow x=-4 \Rightarrow N(-4; 0)\).
Đồ thị hàm số \(y = \dfrac{1}{2}x + 2\) là đường thẳng đi qua hai điểm \(M(0; 2)\) và \(N(-4; 0)\)
+) Hàm số \(y = -x + 2\):
Cho \(x=0 \Rightarrow y=0 + 2=2 \Rightarrow M(0; 2)\).
Cho \(y=0 \Rightarrow 0=-x + 2 \Rightarrow x= 2 \Rightarrow P(2; 0)\).
Đồ thị hàm số \(y = -x + 2\) là đường thẳng đi qua hai điểm \(M(0; 2)\) và \(P(2; 0)\)
b) +) Hoành độ điểm \(C\) là nghiệm của phương trình:
\(\dfrac{1}{2}x+2=-x+2\)
\(\Leftrightarrow \dfrac{1}{2}x+x=2-2\)
\(\Leftrightarrow x=0\)
Do đó tung độ của \(C\) là: \(y=0+2=2\). Vậy \(C(0; 2) \equiv M\).
+) Vì \(A\) thuộc trục hoành (\(Ox)\) nên tung độ của \(A\) bằng \(0\). Thay \(y=0\) vào \(y=\dfrac{1}{2}x+2\), ta được:
\(0=\dfrac{1}{2}x+2\)
\(\Leftrightarrow \dfrac{1}{2}x=-2\)
\(\Leftrightarrow x=-4\)
Vậy \(A(-4; 0) \equiv N\).
+) Vì \(B\) thuộc trục hoành (\(Ox)\) nên tung độ của \(B\) bằng \(0\). Thay \(y=0\) vào \(y=-x+2\), ta được:
\(0=-x+2\)
\(\Leftrightarrow x=2\)
Vậy \(B(2; 0) \equiv P\).
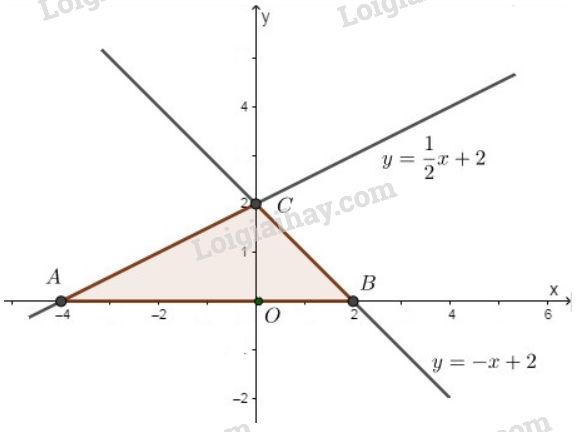
Ta dễ dàng tính được \(OA=4,\ OB=2,\ OC=2,\ AB=6\).
Ta có: \(OB=OC\) nên tam giác \(COB\) vuông cân tại \(O\) (\(O\) là gốc tọa độ) nên: \(\widehat{B}=45^o\)
Dùng công thức lượng giác đối với tam giác \(AOC\) vuông tại \(O\), ta có:
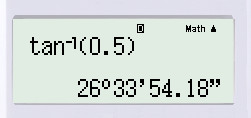
\(\tan A=\dfrac{OC}{OA}=\dfrac{2}{4}=\dfrac{1}{2}\)
Thực hiện bấm máy tính, ta được: \(\widehat{A} \approx 27^o\)
Xét \(\Delta{ABC}\) có: \(\widehat{A}+ \widehat{B}+\widehat{C}=180^o\)
\(\Leftrightarrow \widehat{C}=180^o-\widehat{A}-\widehat{B}\)
\(\Leftrightarrow \widehat{C} \approx 180^o-27^o-45^o\)
\(\Leftrightarrow \widehat{C} \approx 108^o\)
c) Ta có: \(AB = 6 (cm)\)
Xét tam giác vuông \(OAC\) vuông tại \(O\), theo định lí Py-ta-go, ta có:
\(AC^2=AO^2+OC^2=4^2+2^2=16+4=20\)
\(\Rightarrow AC =\sqrt{20}=2\sqrt{5}(cm)\)
Xét tam giác vuông \(OBC\) vuông tại \(O\), ta có:
\(BC^2=BO^2+OC^2=2^2+2^2=4+4=8\)
\(\Rightarrow BC =\sqrt 8 = 2\sqrt{2}(cm)\)
\(\Delta{OAC}\) có \(CO \bot AB\) nên \(CO\) là đường cao ứng với cạnh \(AB\).
Chu vi tam giác là:
\(P=AB+BC+AC=6+2\sqrt{5}+2\sqrt{2} (cm)\)
Diện tích tam giác là:
\(S=\dfrac{1}{2}.OC.AB=\dfrac{1}{2}.2.6=6 (cm^2)\)