Bài 3.45 trang 132 SBT hình học 12

Đề bài

Cho hai đường thẳng d₁: \(\dfrac{{x - 1}}{2} = \dfrac{{y + 2}}{{ - 3}} = \dfrac{{z - 5}}{4}\) và d₂: \(\left\{ {\begin{array}{*{20}{c}}{x = 7 + 3t}\\{y = 2 + 2t}\\{z = 1 - 2t}\end{array}} \right.\)

a) Chứng minh rằng d₁ và d₂ cùng nằm trong một mặt phẳng \((\alpha )\).

b) Viết phương trình của \((\alpha )\).

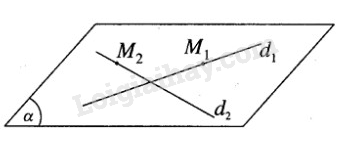
a) Ta có \(\overrightarrow {{u_{{d_1}}}}  = \left( {2; - 3;4} \right)\) và \(\overrightarrow {{u_{{d_2}}}}  = (3;2; - 2)\)

\(\overrightarrow n  = \left[ {\overrightarrow {{u_{{d_1}}}} ,\overrightarrow {{u_{{d_2}}}} } \right] = ( - 2;16;13)\)

Lấy điểm M₁(1; -2; 5) trên d₁ và điểm M₂(7;2;1) trên d₂.

Ta có \(\overrightarrow {{M_1}{M_2}}  = (6;4; - 4)\); \(\overrightarrow n .\overrightarrow {{M_1}{M_2}}  =  - 12 + 64 - 52 = 0\)

Suy ra \({d_1}\) và \({d_2}\) cùng nằm trong mặt phẳng \((\alpha )\)

b) Mặt phẳng \((\alpha )\) chứa \({M_1}\) và có vecto pháp tuyến là \(\overrightarrow n \) , vậy phương trình của \((\alpha )\) là:

\(– 2(x – 1)  +16(y + 2) + 13(z – 5) = 0\)  hay \(2x – 16y – 13z + 31 = 0\).