Bài 40 trang 142 SBT toán 7 tập 1

Đề bài

Qua trung điểm \(M\) của đoạn thẳng \(AB\), kẻ đường thẳng vuông góc với \(AB.\) Trên đường thẳng đó lấy điểm \(K.\) Chứng minh rằng \(KM\) là tia phân giác của góc \(AKB.\)

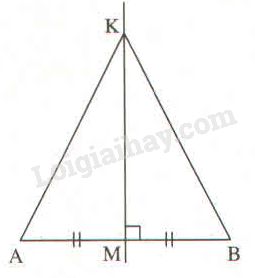
Xét \(∆AMK\) và \(∆BMK\), ta có:

\(AM = BM\) (vì \(M\) là trung điểm của \(AB\))

\(\widehat {AMK} = \widehat {BMK} = 90^\circ \) (vì \(KM \bot AB\))

\(MK\) cạnh chung

\( \Rightarrow ∆AMK = ∆BMK\) (c.g.c)

\(\Rightarrow \widehat {AKM} = \widehat {BKM}\) (hai góc tương ứng).

Vậy \(KM \) là tia phân giác của \(\widehat {AKB}\).