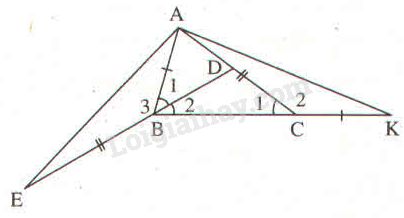
Ta có: \(\displaystyle \widehat B = 2\widehat {{C_1}}\left( {gt} \right) \Rightarrow \widehat {{C_1}} = {1 \over 2}\widehat B\)
Mặt khác: \(\displaystyle \widehat {{B_1}} = \widehat {{B_2}}={1 \over 2}\widehat B\) (vì \(BD\) là tia phân giác góc \(B\))
\( \Rightarrow \widehat {{C_1}} = \widehat {{B_1}}\) (1)
\(\widehat {{C_1}} + \widehat {{C_2}} = 180^\circ \) (hai góc kề bù) (2)
\(\widehat {{B_1}} + \widehat {{B_3}} = 180^\circ \) (hai góc kề bù) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {{C_2}} = \widehat {{B_3}}\)
Xét \(∆ABE\) và \(∆ KCA\), ta có:
\(AB = KC\) (gt)
\(\widehat {{B_3}} = \widehat {{C_2}}\) (chứng minh trên)
\(BE = CA\) (gt)
\( \Rightarrow ∆ABE = ∆ KCA\) (c.g.c)
\( \Rightarrow AE = AK\) (hai cạnh tương ứng).