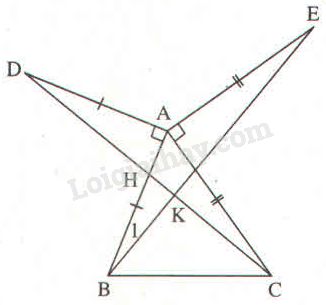
a)
\(\eqalign{
& \widehat {BA{\rm{E}}} = \widehat {BAC} + 90^\circ \cr
& \widehat {CA{\rm{D}}} = \widehat {BAC} + 90^\circ \cr
& \Rightarrow \widehat {BA{\rm{E}}} = \widehat {CA{\rm{D}}} \cr} \)
Xét \(∆ABE\) và \(∆ADC\), ta có:
\(AB = AD\) (gt)
\(AE = AC\) (gt)
\( \widehat {BA{\rm{E}}} = \widehat {CA{\rm{D}}}\)
\(\Rightarrow ∆ABE = ∆ADC\) (c.g.c)
\(\Rightarrow BE= DC\) (hai cạnh tương ứng)
b) Gọi giao điểm \(DC\) và \(AB\) là \(H\), giao điểm của \(CD\) và \(BE\) là \(K\)
Ta có: \(∆ABE = ∆ADC\) (chứng minh trên)
\(\Rightarrow \widehat {ABE} = \widehat D\) (1)
Xét tam giác vuông \(AHD\) có \(\widehat {HA{\rm{D}}} = 90^\circ \)
\( \Rightarrow \widehat D + \widehat {AH{\rm{D}}} = 90^\circ \) (tính chất tam giác vuông) (2)
Mà: \(\widehat {AH{\rm{D}}} = \widehat {KHB}\) (đối đỉnh) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {ABE} + \widehat {KHB} = 90^\circ \) hay \(\widehat {HBK} + \widehat {KHB} = 90^\circ \)
Áp dụng định lí tổng các góc của một tam giác vào \(∆KHB\), ta có:
\(\widehat {KHB} + \widehat {HBK} + \widehat {BKH} = 180^\circ \)
\( \Rightarrow \widehat {BKH} = 180^\circ - \left( {\widehat {HBK} + \widehat {KHB}} \right)\)\(\, = 180^\circ - 90^\circ = 90^\circ \)
Vậy \(DC \bot BE\).