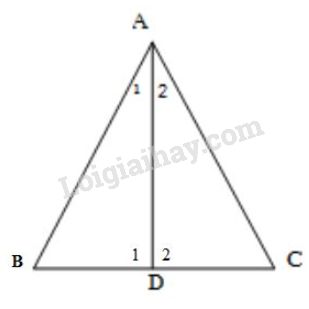
a) Áp dụng định lí tổng các góc của một tam giác vào \(\Delta ABD\) và \(\Delta ACD\) ta có:
\(\begin{gathered} \widehat B + \widehat {{A_1}} + \widehat {{D_1}} = {180^o}\,\,\,(1) \hfill \\ \widehat C + \widehat {{A_2}} + \widehat {{D_2}} = {180^o}\,\,\,(2) \hfill \\ \end{gathered} \)
\(\widehat{ B} = \widehat{ C}\) (gt) (3)
\(\widehat{ A_{1}}= \widehat{ A_{2}}\) (vì \(AD\) là tia phân giác góc \(A\)) (4)
Từ (1), (2), (3), (4) suy ra \(\widehat{ D_{1}} = \widehat{ D_{2}}\)
Xét \(∆ADB\) và \(∆ ADC\) có:
+) \(\widehat{ A_{1}}= \widehat{ A_{2}}\) (chứng minh trên)
+) \(\widehat{ D_{1}} = \widehat{ D_{2}}\) (chứng minh trên)
+) \(AD\) cạnh chung
\( \Rightarrow ∆ADB = ∆ADC \) (g.c.g)
b) \(∆ADB = ∆ADC\) (chứng minh câu a)
\( \Rightarrow AB=AC\) (hai cạnh tương ứng).