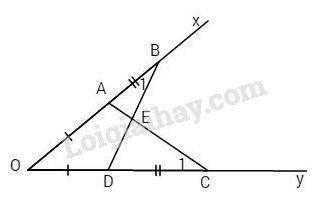
a) Xét \(\Delta AOC\) và \(\Delta DOB\) có:
+) \(OA = OD\) (giả thiết)
+) \(\widehat O\) chung
+) \(OC = OB\) (giả thiết)
Do đó \(\Delta AOC=\Delta DOB\) (c.g.c)
\( \Rightarrow AC = BD\) (cạnh tương ứng).
b) Ta có \(OB = OC\) (giả thiết)
\(OA = OD\) (giả thiết)
\( \Rightarrow OB - OA = OC - OD\)
Hay \(AB = CD\) (1)
Lại có \(\widehat {OAC} + \widehat {CAB} = {180^o}\) (kề bù).
Tương tự \(\widehat {ODB} + \widehat {BDC} = {180^o}\).
Mà \(\widehat {OAC} = \widehat {ODB}\,\left( {\Delta AOC = \Delta DOB} \right) \)
\(\Rightarrow \widehat {CAB} = \widehat {BDO}\,\,\,(2)\).
Mặt khác \(\widehat {{B_1}} = \widehat {{C_1}}\,\left( {\Delta AOC = \Delta DOB} \right)\,\,\,(3)\)
Do đó từ (1), (2) và (3) ta có \(\Delta EAB = \Delta EDC\) (g.c.g)