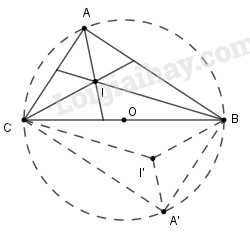
Điểm A luôn nhìn đoạn thẳng AB dưới một góc \(90^\circ \) nên quỹ tích điểm \(A\) là đường tròn đường kính \(BC.\)
Xét tam giác \(ABC\) vuông tại \(A\) nên \(\widehat {ACB} + \widehat {ABC} = 90^\circ \), lại có \(BI\) là phân giác góc \(B\) và \(CI\) là phân giác góc \(C\) nên
\(\widehat {ICB} = \dfrac{1}{2}\widehat {ACB};\,\widehat {IBC} = \dfrac{1}{2}\widehat {ABC} \Rightarrow \widehat {ICB} + \widehat {IBC} = \dfrac{1}{2}\left( {\widehat {ACB} + \widehat {ABC}} \right) = \dfrac{1}{2}.90^\circ = 45^\circ \)
Xét tam giác \(IBC\) có \(\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = 180^\circ \Leftrightarrow \widehat {BIC} = 180^\circ - 45^\circ = 135^\circ \)
Nên số đo góc \(BIC\) luôn không đổi.
Vậy khi điểm A thay đổi trên đường tròn đường kính BC thì điểm I thay đổi và luôn nhìn đoạn thẳng BC dưới một góc \(135^\circ .\)
Vậy điểm I thuộc hai cung chứa góc \(135^\circ \) dựng trên đoạn BC.
Kết luận: Quĩ tích các điểm I là hai cung chứa góc \(135^\circ \) dựng trên đoạn BC.