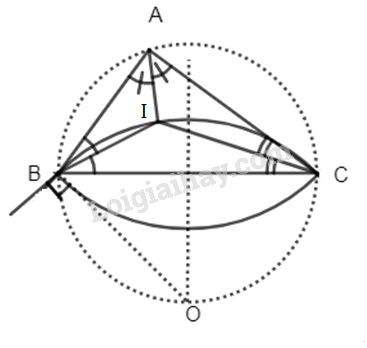
Ta có : \(\widehat A = 90^\circ \Rightarrow \widehat B + \widehat C = 90^\circ \)
\( \Rightarrow {{\widehat B} \over 2} + {{\widehat C} \over 2} = 45^\circ \)
Hay \(\widehat {IBC} + \widehat {ICB} = 45^\circ \). Do đó \(\widehat {BIC} = 135^\circ \).
Vậy I nằm trên cung chứa góc 135º dựng trên đoạn BC ( trừ B và C).
Cách vẽ :
− Vẽ đường trung trực d của đoạn BC.
− Vẽ tia Bx tạo với BC góc 135º.
− Vẽ tia By vuông góc với Bx.
− Lấy O là giao điểm của By với d.
− Vẽ cung BmC tâm O, bán kính OB sao cho cung này nằm ở nửa mặt phẳng bờ BC không chứa tia Bx.
Cung BmC là cung chứa góc 135º dựng trên đoạn BC.
− Lấy O’ đối xứng với O qua BC, ta có cung Bm’C.