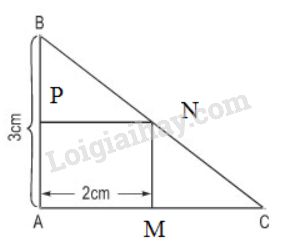
Gọi \(x (cm)\) là độ dài cạnh \(AC (x > 0)\).
Gọi hình chữ nhật là \(MNPA\) thì \(MC = x – 2 (cm)\)
Vì \(MN // AB\) nên \(\dfrac{{MN}}{{AB}} = \dfrac{{MC}}{{AC}}\) (hệ quả của định lí TaLet)
\( \Rightarrow MN = \dfrac{{AB.MC}}{{AC}} = \dfrac{{3\left( {x - 2} \right)}}{x}(cm)\)
Diện tích hình chữ nhật \(MNPA\) là: \(2.\dfrac{{3\left( {x - 2} \right)}}{x} = \dfrac{{6\left( {x - 2} \right)}}{x}\)
Diện tích hình tam giác \(ABC\) là: \(\dfrac{1}{2}AB.AC = \dfrac{1}{2}.3.x = \dfrac{3}{2}x\)
Vì diện tích hình chữ nhật \(MNPA\) bằng một nửa diện tích hình tam giác \(ABC\) nên ta có phương trình:
\(\eqalign{
& {3 \over 2}x = 2.{{6\left( {x - 2} \right)} \over x} \cr
& \Leftrightarrow {{3x.x} \over {2x}} = {{2.2.6\left( {x - 2} \right)} \over {2x}} \cr
& \Rightarrow 3{x^2} = 24x - 48 \cr
& \Leftrightarrow 3{x^2} - 24x + 48 = 0 \cr
& \Leftrightarrow {x^2} - 8x + 16 = 0 \cr
& \Leftrightarrow {x^2} - 2.x.4 + {4^2} = 0 \cr
& \Leftrightarrow {\left( {x - 4} \right)^2} = 0 \cr
& \Leftrightarrow x - 4 = 0 \cr
& \Leftrightarrow x = 4\text{ (thỏa mãn)} \cr} \)
Vậy \(AC = 4cm\).