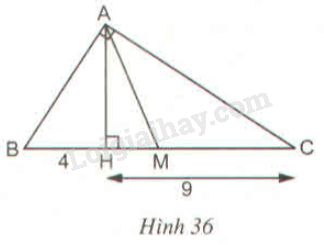
Xét hai tam giác vuông \(HBA\) và \(HAC\) có:
\(\widehat {BHA} = \widehat {AHC} = 90^\circ \)
\(\widehat {HBA} = \widehat {HAC}\) (vì hai góc cùng phụ với \(\widehat C\))
\( \Rightarrow ∆ HBA \backsim ∆ HAC\) (g.g)
\( \Rightarrow \displaystyle {{HA} \over {HB}} = {{HC} \over {HA}}\)
\( \Rightarrow H{A^2} = HB.HC = 4.9 = 36\)
\( \Rightarrow AH = 6\;(cm)\).
Vì \(AM\) là trung tuyến nên \(M\) là trung điểm của \(BC\) do đó \(\displaystyle BM = {1 \over 2}BC = {1 \over 2}.\left( {9 + 4} \right) \)\(\,=6,5\; (cm)\)
Mà \(HM = BM - BH = 6,5 - 4 \)\(\,= 2,5\; (cm)\).
Vậy \(\displaystyle {S_{AHM}} = {1 \over 2}AH.HM = {1 \over 2}.6.2,5 \)\(\,= 7,5\,(c{m^2})\).