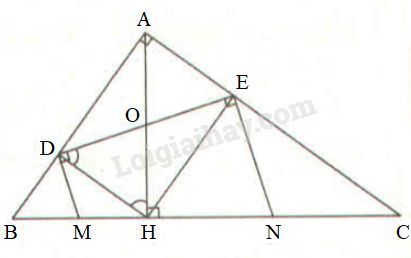
a) Xét hai tam giác vuông \(ABH\) và \(CAH\) có:
\(\widehat {ABH} = \widehat {CAH}\) (cùng phụ với \(\widehat {BAH}\))
\(\widehat {AHB} = \widehat {CHA} = {90^o}\)
\(\Rightarrow ∆ ABH\) đồng dạng \(∆ CAH\) (g.g).
\( \Rightarrow\displaystyle {{AH} \over {CH}} = {{BH} \over {AH}}\)
\( \Rightarrow A{H^2} = BH.CH \)
\(\Rightarrow AH=\sqrt {BH.CH} = \sqrt {4.9} \)\(\,= 6\,(cm) \)
Mặt khác, \(HD ⊥ AB\) và \(HE ⊥ AC\) nên \(ADHE \) là hình chữ nhật.
Suy ra: \(DE = AH = 6 \;(cm)\) (hình chữ nhật có hai đường chéo bằng nhau).
b) Ta có:
\(\begin{array}{l}\widehat {MDH} = {90^o} - \widehat {ODH}\\\widehat {MHD} = {90^o} - \widehat {OHD}\end{array}\)
Mà \(ADHE \) là hình chữ nhật nên \(\widehat {ODH} = \widehat {OHD}\).
Do đó \(\widehat {MDH} = \widehat {MHD}\).
Xét tam giác \(MDH\) có \(\widehat {MDH} = \widehat {MHD}\) (chứng minh trên) nên \(\Delta MDH\) cân tại \(M\), do đó \(MD = MH\) (1)
\(\begin{array}{l}\widehat {BDM} + \widehat {MDH} = {90^o}\\\widehat {MDH} = \widehat {MHD}\,\,(cmt)\\ \Rightarrow \widehat {BDM} + \widehat {MHD} = {90^o}\end{array}\)
Mặt khác: \(\widehat {MBD} + \widehat {MHD} = {90^o}\) (hai góc nhọn trong tam giác vuông phụ nhau)
Do đó: \( \widehat {BDM} = \widehat {MBD}\)
Suy ra \(\Delta BDM\) cân tại \(M\) nên \(MD = BM\) (2)
Từ (1) và (2) suy ra \(M \) là trung điểm của \(BH\).
Chứng minh tương tự \(N\) là trung điểm của \(CH.\)
c) Theo chứng minh trên, ta có:
\(DM = MH \displaystyle= {1 \over 2}BH = \displaystyle{1 \over 2}.4 = 2(cm) \)
\(EN = NH \displaystyle= {1 \over 2}CH =\displaystyle {1 \over 2}.9 = 4,5\)\(\,(cm) \)
\(DE = AH = 6\,(cm) \)
\(DENM \) là hình thang vuông, do đó diện tích của nó là:
\(\displaystyle {S_{DENM}} = {1 \over 2}\left( {DM + EN} \right)DE \)\(\,\displaystyle = {1 \over 2}.\left( {2 + 4,5} \right).6 = 19,5\,(c{m^2})\).