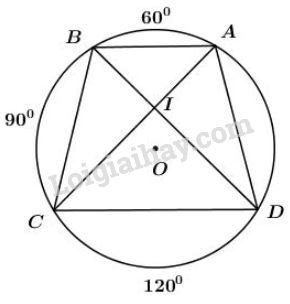
a) Xét đường tròn \((O)\) ta có:
\(\displaystyle \widehat {BA{\rm{D}}} = {{{{90}^0} + {{120}^0}} \over 2} = {105^0}\) (góc nội tiếp chắn \(\overparen{BCD}\)) (1)
\(\displaystyle \widehat {A{\rm{D}}C} = {{{{60}^0} + {{90}^0}} \over 2} = {75^0}\) ( góc nội tiếp chắn\(\overparen{ABC}\) ) (2)
Từ (1) và (2) có:
\(\widehat {BA{\rm{D}}} + \widehat {A{\rm{D}}C} = {105^0} + {75^0} = {180^0}\) (3)
\(\widehat {BA{\rm{D}}}\) và \(\widehat {A{\rm{D}}C}\) là hai góc trong cùng phía tạo bởi cát tuyến \(AD\) và hai đường thẳng \(AB, CD.\)
Đẳng thức (3) chứng tỏ \(AB // CD\). Do đó tứ giác \(ABCD\) là hình thang, mà hình thang nội tiếp đường tròn là hình thang cân.
Vậy \(ABCD\) là hình thang cân suy ra (\(BC = AD\) và \(sđ\overparen{BC}\)=\(sđ\overparen{AD}\)=\(90^0\))
b) Giả sử hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(I\).
\(\widehat {CI{\rm{D}}}\) là góc có đỉnh nằm trong đường tròn, nên:
\(\displaystyle \widehat {CI{\rm{D}}}\) \(=\dfrac{sđ\overparen{AB}+sđ\overparen{CD}}{2}\)\(=\displaystyle {{{{60}^0} + {{120}^0}} \over 2} = {90^0}\)
Vậy \(AC \bot BD.\)
c) Vì \(sđ\overparen{AB}= 60^0\) nên \(\widehat {AOB} = {60^0}\) (góc ở tâm)
\(=> ∆AOB\) đều, nên \(AB = OA = OB = R.\)
Vì \( sđ \overparen{BC} = {90^0} \Rightarrow \widehat {BOC} = {90^0}\) (góc ở tâm)
\(\Rightarrow BC = \sqrt{OB^2+OC^2}=R\sqrt2.\)
Kẻ \(OH \bot CD.\)
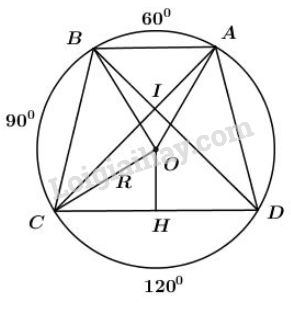
Tứ giác \(ABCD\) là hình thang cân \(\Rightarrow \widehat{BCD}=\widehat{ADC}=75^0.\)
Lại có \(\Delta BOC\) vuông cân tại \(O \Rightarrow \widehat{BCO}=45^0.\)
\(\Rightarrow \widehat{OCD}=\widehat{BCD}-\widehat{BCO}=75^0-45^0=30^0.\)
Xét \(\Delta OCH\) vuông tại \(H\) ta có:
\(HC=OC.\cos \widehat{OCH}=\dfrac{R\sqrt{3}}{2}.\)
Mà \(H\) là trung điểm của \(CD\) (định lý đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy).
\(\Rightarrow CD=2.CH=\sqrt3.\)