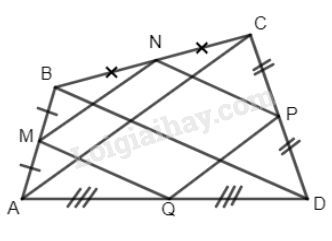
a) Ta có MN là đường trung bình của \(\Delta ABC\)
\( \Rightarrow MN// AC\) và \(MN = {1 \over 2}AC\)
Tương tự \(QP//AC\) và \(QP = {1 \over 2}AC\)
Do đó \(MN// QP\) và MN = QP
Vậy tứ giác MNPQ là hình bình hành.
b) Ta có: \({S_{BMN}} = \dfrac{1 }{ 4}{S_{ABC}};{S_{DPQ}} = \dfrac{1 }{4}{S_{ACD}}\)
\( \Rightarrow {S_{BMN}} + {S_{DPQ}} = \dfrac{1 }{ 4}\left( {{S_{ABC}} + {S_{ACD}}} \right) \)\(\,= \dfrac{1 }{ 4}{S_{ABCD.}}\)
Tương tự \({S_{CNP}} + {S_{AMQ}} = \dfrac{1 }{4}{S_{ABCD}}\)
Do đó: \({S_{BMN}} + {S_{DQP}} + {S_{CNP}} + {S_{AMQ}} \)\(\,= \dfrac{1}{2}{S_{ABCD}}.\)
Vậy: \({S_{MNPQ}} = \dfrac{1 }{ 2}{S_{ABCD.}}\)