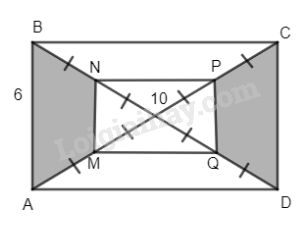
a) Ta có MN và PQ lần lượt là các đường trung bình của các tam giác AOB và COD mà \(AB// CD\) và AB = CD nên \(MN// PQ\) và MN = PQ.
Tương tự \(NP//BC\) mà \(AB \bot BC\) nên \(MN \bot NP.\) Do đó MNPQ là hình chữ nhật.
Trong \(\Delta ABC\) ta có:
\(BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} \)\(\,= 8\left( {cm} \right)\) (định lý py – ta – go)
Nên \(MN = {1 \over 2}AB = 3cm,\) \(NP = {1 \over 2}BC = 4cm\)
Vậy \({S_{MNPQ}} = MN.NP = 3.4 = 12\left( {c{m^2}} \right)\)
b) Dễ thấy \(\Delta AOB = \Delta COD\left( {c.c.c} \right),\) tương tự \(\Delta MON = \Delta POQ.\)
Do đó: \({S_{AOB}} = {S_{COD}}\) và \({S_{MON}} = {S_{POQ}}\)
\( \Rightarrow {S_{AOB}} - {S_{MON}} = {S_{COD}} - {S_{POQ}}\) hay \({S_{AMNB}} = {S_{CPQD}}.\)