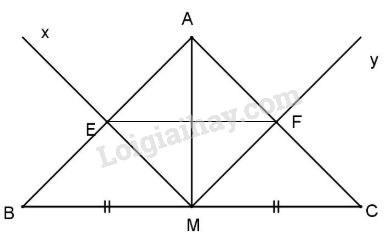
a) Mx // AC (gt) \( \Rightarrow \widehat {{M_1} = \widehat C}\) (đồng vị); tương tự My // AB \( \Rightarrow {\widehat M_2} = \widehat B\) mà \(\widehat B = \widehat C\) (gt)
\(\widehat B = \widehat C = {\widehat M_1} = {\widehat M_2},\) lại có MB = MC (gt)
Do đó \(\Delta BME = \Delta CMF\) (g.c.g)
\( \Rightarrow ME = MF\) và \(BE = CF.\)
b) Ta có: \(AB = CF\) (gt); \(BE = CF\) (cmt)
\( \Rightarrow AB - BE = AC - CF\) hay \(A{\rm{E}} = AF\).
Lại có \(ME = MF\) (cmt). Do đó AM là đường trung trực của EF.