Đề kiểm tra 45 phút ( 1 tiết) - Đề số 1 - Chương 1 - Hình học 8

Bài 1. Cho hình thoi ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.

a) Chứng minh \(\Delta AOM = \Delta CON\).

b) Chứng tỏ tứ giác AMCN là hình bình hành.

Bài 2. Cho tam giác ABC vuôn tại A có đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối  xứng với M qua D.

a) Chứng minh tứ giác AEBM là hình thoi.

b) Gọi I là trung điểm AM. Chứng minh E, I, C thẳng hàng.

c) \(\Delta ABC\) có thêm điều kiện gì thì AEBM là hình vuông.

 Bài 1.

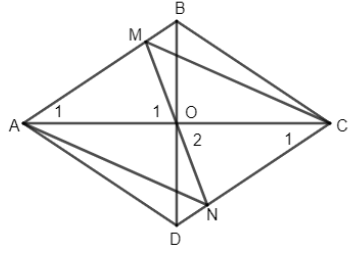
a) Ta có \(\widehat {{A_1}} = \widehat {{C_1}}\) (so le trong)

AO = CO (tính chất đường chéo hình thoi)

\(\widehat {{O_1}} = \widehat {{O_2}}\)

Vậy \(\Delta AOM = \Delta CON\left( {c.g.c} \right)\)

suy ra \( OM = ON.\)

b) Xét tứ giác AMCN có OM = ON (cmt), OA = OC (gt)

Do đó AMCN là hình bình hành. 

Bài 2.

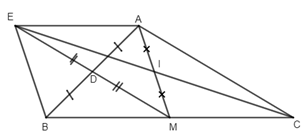
a) Ta có DA = DB, DE = DM (tính chất đối xứng)

\( \Rightarrow AEBM\) là hình bình hành.

Lại có MA = BM (trung tuyến tam giác vuông bằng nửa cạnh huyển).

Vậy AEBM là hình thoi.

b) Ta có \(AE//BM\) và AE = BM (vì AEBM là hình thoi) mà MC = BM 

\( \Rightarrow AE//MC\) và \(AE = MC.\)

Do đó tứ giác AEMC là  hình bình hành, I là trung điểm của đường chéo AM nên đường chéo thứ hai EC phải qua I hay ba điểm E, I, C thằng hàng.

c) Hình thoi AEBM là hình vuông \( \Leftrightarrow AB = EM\) hay EM = AC

\( \Leftrightarrow AB = AC \Leftrightarrow \Delta ABC\) vuông cân