Ta có \(12\) hình viên phân có diện tích bằng nhau tạo nên cánh hoa đó.
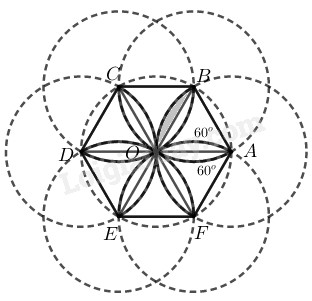
Xét hình viên phân giới hạn bởi cung \(\overparen{BO}\) và dây căng cung đó thì cung \(\overparen{BO}\) là cung của đường tròn tâm \(A\) bán kính \(R.\)
\(OA = AB = OB = R\)
\( \Rightarrow \Delta AOB\) đều \( \Rightarrow \widehat {OAB} = {60^0}\)
Diện tích hình quạt \(AOB\) là:
\(S'=\displaystyle {{\pi {R^2}.60} \over {360}} = {{\pi {R^2}} \over 6}\)
Kẻ \(AI \bot BO\). Trong tam giác vuông \(AIO\) ta có:
\(AI = AO. \sin\widehat {AOI} \)\(= R.\sin {60^0} = \displaystyle {{R\sqrt 3 } \over 2}\)
\(S_{\Delta AOB}=\displaystyle {1 \over 2}AI.AB \)\(= \displaystyle {1 \over 2}.{{R\sqrt 3 } \over 2}.R = {{{R^2}\sqrt 3 } \over 4}\)
Diện tích \(1\) hình viên phân là:
\(S_1=S'-S_{\Delta AOB}\)
\(=\displaystyle {{\pi {R^2}} \over 6} - {{{R^2}\sqrt 3 } \over 4} = {{2\pi {R^2} - 3{R^2}\sqrt 3 } \over {12}}\)
Diện tích của hình cánh hoa:
\(S = 12. S_1 = 12.\displaystyle {{2\pi {R^2} - 3\displaystyle {R^2}\sqrt 3 } \over {12}}\)\( = {R^2}\left( {2\pi - 3\sqrt 3 } \right)\) (đơn vị diện tích)