\(∆ABC\) nội tiếp trong đường tròn \((O)\) có ba khả năng xảy ra của tam giác
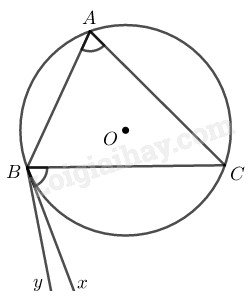
- \(∆ABC\) là tam giác nhọn
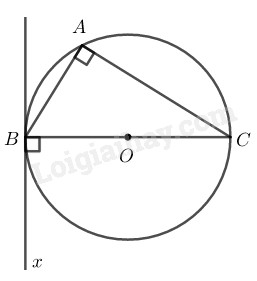
- \(∆ABC\) là tam giác vuông
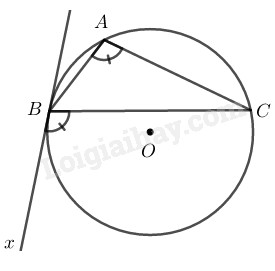
- \(∆ABC\) là tam giác tù
Xét trường hợp \(∆ABC\) là tam giác nhọn
Giả sử \(Bx\) không phải là tiếp tuyến của đường tròn \((O).\) Trên cùng nửa mặt phẳng bờ đường thẳng \(BC\) chứa tia \(Bx\) ta kẻ tia \(By\) là tiếp tuyến của đường tròn \((O)\)
\( \Rightarrow \widehat {CBy} = \widehat {BAC}\) (hệ quả của góc giữa tia tiếp tuyến và dây cung)
\(\widehat {CBx} = \widehat {BAC}\) \((gt)\)
Suy ra: \(\widehat {CBy} = \widehat {CBx}\)
Ta có \(By\) và \(Bx\) là hai tia khác nhau từ nằm trên cùng một nửa mặt phẳng bờ \(BC\) tạo với \(BC\) một góc bằng nhau với tính chất đặt tia trên nửa mặt phẳng. Mâu thuẫn với giả sử \(Bx\) không phải là tiếp tuyến của đường tròn \((O).\) Vậy \(Bx\) là tiếp tuyến của đường tròn \((O).\)