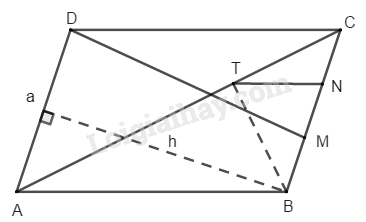
a) \(∆ DMC\) có \(CM = \dfrac{2}{3}BC\)
Hình bình hành \(ABCD\) và \(∆ DMC\) có chung đường cao kẻ từ đỉnh \(D\) đến \(BC.\)
Gọi độ dài đường cao là \(h,\, BC = a\)
Ta có diện tích hình bình hành \(ABCD\) là \(S = a. h\)
\(\begin{array}{l}{S_{DMC}} = \dfrac{1}{2}h.\dfrac{2}{3}a = \dfrac{1}{3}ah = \dfrac{1}{3}S\\{S_{ABMD}} = {S_{ABCD}} - {S_{DMC}}\\ = S - \dfrac{1}{3}S = \dfrac{2}{3}S\end{array}\)
b) \({S_{ABC}} =\eqalign {1 \over 2}{S_{ABCD}} = \eqalign{S \over 2}\)
\(CN = \eqalign{1 \over 3}BC,\) \(NT // AB.\)
Theo tính chất đường thẳng song song cách đều \( \Rightarrow CT = \eqalign{1 \over 3}AC\)
\(∆ ABC\) và \(∆ BTC\) có chung chiều cao kẻ từ đỉnh \(B,\) đáy \(CT = \eqalign{1 \over 3}AC\)
\( \Rightarrow {S_{BTC}} = \eqalign{1 \over 3}{S_{ABC}} = \eqalign{1 \over 3}.\eqalign{S \over 2} = \eqalign{S \over 6}\)
\(∆ BTC\) và \(∆ TNC\) có chung chiều cao kẻ từ đỉnh \(T,\) cạnh đáy \(CN = \eqalign{1 \over 3}CB\)
\(\begin{array}{l} \Rightarrow {S_{TNC}} = \dfrac{1}{3}{S_{BTC}} = \dfrac{1}{3}.\dfrac{S}{6} = \dfrac{S}{{18}}\\ \Rightarrow {S_{ABNT}} = {S_{ABC}} - {S_{TNC}}\\ = \dfrac{S}{2} - \dfrac{S}{{18}} = \dfrac{{4S}}{9}\end{array}\)