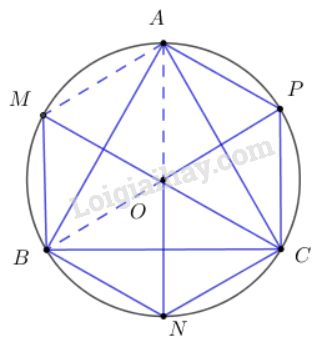
a) Nối \(OC\) và kéo dài cắt đường tròn tại điểm \(M\)
Dễ thấy, tam giác \(OAM\) là tam giác đều và \(OAMB\) là hình bình hành, cho ta:
\(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OM} \)
b) Nối \(OB\) và kéo dài cắt đường tròn tại điểm \(P\)
Tương tự như trên ta có:
\(\overrightarrow {OP} = \overrightarrow {OC} + \overrightarrow {OA} \)
c) Nối \(OA\) và kéo dài cắt đường tròn tại điểm \(N\)
Tương tự như trên ta có:
\(\overrightarrow {ON} = \overrightarrow {OB} + \overrightarrow {OC} \)