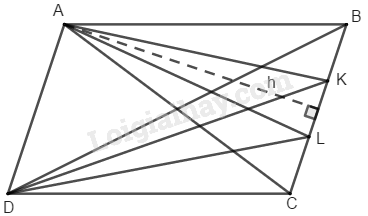
a) Ta có: \({S_{ACD}} = {S_{BCD}} = {S_{DAB}} = {S_{CAB}} \) \(=\eqalign {1 \over 2}{S_{ABCD}}\) (1)
\(CK = \eqalign{1 \over 2}CB\)
\(∆ DCK = ∆ DCB\) có chung chiều cao kẻ từ đỉnh \(D,\) cạnh đáy \(CK = \eqalign{2 \over 3}CB\)
\( \Rightarrow {S_{DCK}} =\eqalign {2 \over 3}{S_{DBC}}\) (2)
Từ (1) và (2) suy ra: \({S_{DCK}} = \eqalign{2 \over 3}{S_{DAC}} \Rightarrow \eqalign{{{S_{DCK}}} \over {{S_{DAC}}}} = \eqalign{2 \over 3}\)
b) Ta có: \({S_{ADLB}} = {S_{ADB}} + {S_{DLB}}\)
\(∆ DBC\) và \(∆ DLC\) có chung chiều cao kẻ từ đỉnh \(D,\) cạnh đáy \(LB =\eqalign {2 \over 3}BC\)
\( \Rightarrow {S_{DLB}} = \eqalign{2 \over 3}{S_{DBC}}\)
mà \({S_{DAC}} = {S_{ADB}} = {S_{DBC}}\) (chứng minh trên)
Suy ra: \({{S_{ADLB}} = {S_{DAC}} + \eqalign{2 \over 3}{S_{DAC}}} \) \({= \eqalign{5 \over 3}{S_{DAC}}} \)
\(\Rightarrow \eqalign{{{S_{DAC}}} \over {{S_{ADLB}}}} = \eqalign{3 \over 5}\)
c) Ta có: \({S_{ABKD}} = {S_{ABD}} + {S_{DKB}}\)
\(∆ DKB\) và \(∆ DCB\) có chung chiều cao kẻ từ \(D,\) cạnh đáy \(BL = \eqalign{1 \over 3}BC\)
\( \Rightarrow {S_{DKB}} = \eqalign{1 \over 3}{S_{DCB}}\)
mà \({S_{DAC}} = {S_{ADB}} = {S_{DBC}}\) (chứng minh trên)
\( \Rightarrow {S_{ABKD}} = {S_{DAC}} + \eqalign{1 \over 3}{S_{DAC}} \) \(=\eqalign {4 \over 3}{S_{DAC}}\)
\(\Rightarrow \eqalign{{{S_{ABKD}}} \over {{S_{ADLB}}}} = \eqalign{{\eqalign{4 \over 3}{S_{DAC}}} \over {\eqalign{5 \over 3}{S_{DAC}}}} = \eqalign{4 \over 5}\)