Đề kiểm tra 45 phút (1 tiết) - Đề số 2 – Chương IV - Giải tích 12
Lời giải
Bài Tập và lời giải
Bài 1: Cho x tỉ lệ thuậ với y theo hệ số tỉ lệ \({1 \over 2}\) và y tỉ lệ thuận với z theo hệ số tỉ lệ \({1 \over 3}\). Chứng tỏ x tỉ lệ thuận với z và tìm hệ số tỉ lệ.
Bài 2: Cho biết x và y tỉ lệ thuận với nhau và khi \(x = 4\) thì \(y = -2\). Tìm hệ số tỉ lệ của k của y đối với x và biểu diễn y theo x.
Đề bài
Bài 1: Cho y tỉ lệ thuận với x theo hệ số tỉ lệ k, với \({x_1};{x_2}\) có hai giá trị tương ứng là \({y_1};{y_2}\) và \({x_1} + {x_2} = 4;{y_1} + {y_2} = 8\). Tìm k.
Bài 2: cho x, y là hai đại lượng tỉ lệ thuận.
Điền số thích hợp vào ô trống trong bảng sau:
|
x |
-2 |
1 |
3 |
|
|
y |
|
-2 |
|
3 |
Đề bài
Bài 1: Cho x và y là hai đại lượng tỉ lệ thuận. điền số thích hợp vào ô trống:
|
x |
|
12 |
1 |
-2 |
|
y |
3 |
-6 |
|
|
Bài 2: Cho hai số có tổng bằng 32 và hai số đó tỉ lệ với 3 và 5.
Đề bài
Bài 1: Cho y tỉ lệ thuận với x theo hệ số tỉ lệ \( - {1 \over 2}\).
Điền vào ô trống:
|
x |
1 |
|
-3 |
|
|
y |
|
2 |
|
5 |
Bài 2: Cho x và y là hai đại lượng tỉ lệ thuận, biết \({x_1} - {x_2} = 2\) và hai giá trị tương ứng \({y_1}\) và \({y_2}\) có \({y_1} - {y_2} = - 1.\) Biểu diễn y theo x.
Đề bài
Bài 1: Hai số tỉ lệ với 25 và 35. Hiệu số của chúng bằng 6. Tìm hai số đó.
Bài 2: Số đo của chu vi hình vuông có phải là đại lượng tỉ lệ thuận với cạnh hình vuông? Tìm hệ số tỉ lệ ( nếu có).
Đề bài
Cho tam giác có ba cạnh tỉ lệ với 3, 4, 5 và chu vi bằng 36cm. Tính độ dài các cạnh của tam giác
Đề bài
Hãy chia 1200kg gạo thành bốn phần tỉ lệ với 2, 3, 7, 13 ( đơn vị : kg).
Đề bài
Cho tam giác ABC có số đo ba góc A, B, C tỉ lệ với 1, 2, 3. Tính số đo ba góc A, B, C của tam giác.
Đề bài
Số học sinh giỏi ở các khối lớp 6, 7, 8, 9 tỉ lệ với 1,5; 1,1; 1,3; 1,2. Biết rằng số học sinh giỏi khối 8 nhiều hơn khối 9 là 3 học sinh.
Tính số học sinh giỏi ở các khối lớp.
Đề bài
Bài 1: Cho x, y là hai đại lượng tỉ lệ nghịch và khi \(x = 7\) thì \(y = 10\).
a) Tìm hệ số tỉ lệ.
b) Biểu diễn y theo x.
c) Tính giá trị của y khi \(x = 5.\)
Bài 2: Cho x, y là hai đại lượng tỉ lệ nghịch. Điền số thích hợp vào ô trống :
|
x |
-2 |
3 |
|
|
y |
|
\( - {1 \over 6}\) |
12 |
Đề bài
Bài 1: Cho ba đại lượng x, y, z. biết x, y tỉ lệ nghịch theo tỉ số \({1 \over 2},\) y tỉ lệ thuận với z theo hệ số tỉ lệ (-2). Chứng tỏ x và z là hai lượng tỉ lệ nghịch. Tìm hệ số tỉ lệ đó.
Bài 2: Cho a, b là hai số tỉ lệ nghịch với 4, 5 và \(b - a = 27.\) Tìm a, b.
Đề bài
Bài 1: Cho x, y là hai số tỉ lệ nghịch với 3; 7 và \(x - y = - 16\) . Tìm x,y.
Bài 2: Cho y tỉ lệ thuận với x theo hệ số tỉ lệ 2 ; y và z tỉ lệ nghịch theo hệ số tỉ lệ -3. Chứng tỏ x và z là hai đại lượng tỉ lệ nghịch. Tìm hệ số tỉ lệ.
Đề bài
Bài 1: Tìm a, b, c biết a, b, c tỉ lệ nghịch với 3, 4, 6 và \(a + b - c = - 20.\)
Bài 2: Cho x và y là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ -3; y và z là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ 2.
Chứng tỏ z tỉ lệ thuận với x. tìm hệ số tỉ lệ.
Đề bài
Bài 1: Tìm ba số x, y, z biết x, y, z tỉ lệ nghịch với 2, 3, 6 và \(x + y + z = 180.\)
Bài 2: Theo x, y, z tỉ lệ nghịch với và \(x + 2y - z = 8.\)
Đề bài
Một bạn học sinh đi xe đạp với vận tốc 12 km/h từ nhà đến trường thì mất nửa giờ. Hỏi nếu bạn đó đi với vận tốc 10 km/h thì từ nhà đến trường mất bao nhiêu thời gian?
Đề bài
Với cùng một số tiền có thể mua 135 mét vải loại I. Có thể mua được bao nhiêu mét vải loại II, biết rằng giá tiền 1 mét vải loại II chỉ bằng 90% giá tiền 1 mét vải loại I.
Đề bài
Có 7 người làm xong một công việc trong 20 ngày. Hỏi 10 người (năng suất như nhau) làm xong công việc trong mấy ngày?
Đề bài
Một ô tô đi từ A đến B với vận tốc 60km/h và trở về A với vận tốc 50km/h. cả đi và về hết 11 giờ. Tính quãng đường. Tính quãng đường AB.
Đề bài
Bài 1: Cho hàm số \(y = f\left( x \right) = \left({ - {1 \over 2}} \right)x\).
a) Tính \(f\left( 2 \right); f\left( 0 \right);f\left( { - 2} \right)\);
b) Tìm x, biết \(f(x) = 2.\)
Bài 2: Cho hàm số y = \(f\left( x \right) = ax - 3\). Tìm a biết \(f(2) = 5.\)
Bài 3: Cho hàm số \(y = f\left( x \right) = ax + b\). Tìm a và b biết \(f(0) = 3\) và f(-1) = 4.
Đề bài
Bài 1: Cho hàm số: \(y = f\left( x \right) = 3 - x.\)
a) Tính \(f\left( { - 2} \right);f\left( { - 1} \right);f\left( 0 \right);f\left( {{1 \over 2}} \right).\)
b) Tìm x biết \(y = 5;2; - 1\).
Bài 2: Cho hàm số: \(y = f\left( x \right) = 3x + m\) .Tìm m biết \(f(1) = -1.\)
Bài 3: Cho hàm số: \(y = f\left( x \right) = ax + b.\) Tìm a, b biết \(f(0) = -3\) và \(f(-1) = -5.\)
Đề bài
Bài 1: Cho hàm số y \(y = f\left( x \right) = \left| {1 - x} \right| + 2.\)
a) Tính \(f\left( { - 1} \right);f\left( 3 \right);f\left( {{3 \over 2}} \right).\)
b) Tìm x biết \(f\left( x \right) = 5;f\left( x \right) = 3.\)
Bài 2: Cho hàm số \(y = f\left( x \right) = ax\). Tìm a biết \(f\left( { - {1 \over 2}} \right) = 3.\)
Bài 3: Cho hàm số \(y = f\left( x \right) = ax + b\). Tìm a, b biết \(f\left( 0 \right) = - 2;f\left( { - {1 \over 2}} \right) = 3.\)
Đề bài
Bài 1: Cho hàm số: \(y = f(x) = ax - 1\). Tìm a biết \(f\left( 2 \right) = 0.\)
Bài 2: Cho hàm số: \(y = f(x) = - 2x + 3\). Tính \(f\left( { - {1 \over 2}} \right);f\left( { - 5} \right);f\left( 3 \right).\)
Bài 3: Cho hàm số: \(y = f(x) = - {x^2} + 2.\)
a) Tính \(f\left( { - \sqrt 2 } \right);f\left( {\sqrt 2 } \right);f\left( 3 \right).\)
b) Tìm x biết \(f\left( x \right) = - 2.\)
Đề bài
Bài 1: Cho điểm \(A(5;3)\). Đánh dấu vị trí của điểm A và của điểm B đối xứng với điểm A qua trục Ox và xác định tọa độ của điểm B.
Bài 2: Cho các điểm \(A(2;7); B(3;4); C(2;-7); D(-3;-4); \)\(\;E(-2;7).\)
a) Xác định các cặp điểm đối xứng với nhau qua gốc tọa độ.
b) Xác định các cặp điểm đối xứng nhau qua trục tung, trục hoành.
Đề bài
Bài 1: Cho các điểm trên hình vẽ.
Xác định tọa độ của A, B, C, D, E.
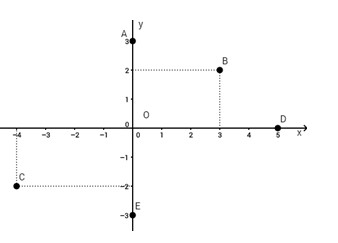
Bài 2: Cho các điểm \(A(2;-2); B(1;1); C(-3;2).\)
Đánh dấu vị trí các điểm A, B, C và các điểm \(A';B';C'\) đối xứng thứ tự với A, B, C
Qua trục Oy. Xác định tọa độ của \(A';B';C'\)
Đề bài
Bài 1: Đánh dấu vị trí các điểm \(A(5;0); B(-5;3) C(0;3); D(-3;1);\)\(\; E(4;2)\). Xác định tọa độ của các điểm đối xứng với A; B; C; D; E qua gốc tọa độ.
Bài 2: Cho ba đỉnh của hình vuông ABCD là \(A(1;2); B(4;2); C(4;5)\). Vẽ hình vuông ABCD. Tìm tọa độ của đỉnh D.
Đề bài
Bài 1: Vẽ tam giác ABC, biết \(A(-3;2); B(3;2); C-1;0).\)
Bài 2: Đánh dấu vị trí của các điểm \(A(5;4); B(2;1); C(-3;2); D(-4;-4)\) và các điểm đối xứng của A, B, C, D qua trục Ox và xác định tọa độ của chúng.
Đề bài
Bài 1: Trên hình vẽ, hãy cho biết tọa độ của A, B, C, D.
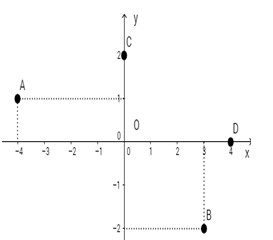
Bài 2: Đánh dấu vị trí các điểm \(A(-2;0)\); \(B(-2;3); C(0;3)\) và dựng hình chữ nhật có ba đỉnh liên tiếp ABC. Tìm tọa độ đỉnh thứ tư.
Bài 3: Vẽ đường phân giác của góc phần tư thứ I và III.
a) Đánh dấu điểm A trên đường phân giác và có hoành độ -3
b) Tìm tung độ của điểm A. Đánh dấu điểm B trên đường phân giác và có tung độ 2. Tìm hoành độ của B.
Đề bài
Bài 1: Những điểm nào sau đây thuộc đồ thị hàm số \(y = {1 \over 2}x\) ?
\(A(5; - 3);B\left( { - 3;4} \right);C(2;1);\) \(D\left( { - 5;{5 \over 2}} \right)\)
Bài 2: Cho hàm số \(y = ax\). Tìm a, biết đồ thị của nó đi qua điểm \(M\left( {{5 \over 2}; - 5} \right).\)
Bài 3: Vẽ đồ thị hàm số \(y = kx\), biết điểm \(A(2;-3)\) thuộc đồ thị cảu hàm số.
Đề bài
Bài 1: Đường thẳng cho trên hình vẽ là đồ thị của hàm số cho bởi công thức nào?
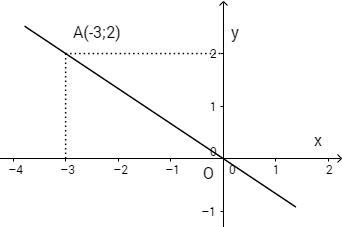
Bài 2: Đường thẳng OA qua gốc tọa độ và điểm \(A\left( {{1 \over 2};7} \right)\) là đồ thị của hàm số nào sau đây: \(y = 7x;y = 14x;y = - 14x\)?
Bài 3: Cho hàm số \(y = ax\). Tìm a biết đồ thị của hàm số qua điểm \(M(-1 ;2)\).
Đề bài
Bài 1: Đánh dấu vị trí hai điểm \(A(1;-2); B(2;-4)\) trên hệ trục tọa độ Oxy. Chứng tỏ O, A, B thẳng hàng.
Bài 2: Cho đồ thị \(y = ax\) trên hình vẽ. Hãy xác định dấu của a.
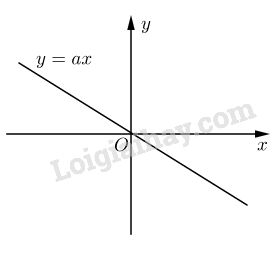
Đề bài
Bài 1: Vẽ đồ thị của hàm số \(y = ax\), biết đồ thị đi qua điểm \(A(-2;1)\). Đồ thị của hàm số có đi qua điểm \(B(10;-5)\) không?
Bài 2: Đường thẳng OM trên hình vẽ là đồ thị của hàm số nào?
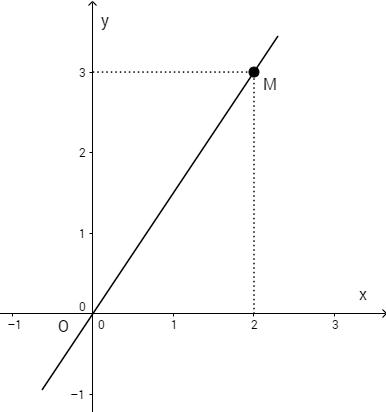
Đề bài
Bài 1: Đánh dấu các điểm \(A(1;3); B(-2;-6); C(-1;-3)\). Chứng tỏ bốn điểm O, A, B,C thẳng hang.
Bài 2: Vẽ đồ thị hàm số \(y = -2x.\) Từ đồ thị hàm số đã vẽ, tìm các giá trị của x khi y dương và y âm.
