Đề kiểm tra 45 phút (1 tiết) - Chương IV - Giải Tích 12
Bài Tập và lời giải
Câu 1. Tìm tập nghiệm S của phương trình \({z^3} + {z^2} - 2 = 0\) trên trường số phức.
A. \(S = \{ - 1 - i,\, - 1 + i\} \).
B. \(S = \{ 1,\,1 - i,\,1 + i\} \).
C. \(S = \{ 1,\, - 1 - i,\, - 1 + i\} \).
D. \(S = \{ 1\} \).
Câu 2. Tính mô đun của số phức \(z\dfrac{{1 + 2i}}{{1 - i}}\).
A. \(|z| = \dfrac{{\sqrt 5 }}{2}\).
B. \(|z| = \sqrt {10} \).
C. \(|z| = \dfrac{5}{2}\).
D. \(|z| = \dfrac{{\sqrt {10} }}{2}\).
Câu 3. Số phức \(z = \dfrac{{1 - i}}{{1 + i}} - 3 + 4i\) có số phức liên hợp là:
A. \(\overline z = - 3i\).
B. \(\overline z = - 3\).
C. \(\overline z = - 3 + 3i\).
D. \(\overline z = - 3 - 3i\).
Câu 4. Trên mặt phẳng tọa độ, để tập hợp điểm biểu diễn các số phức z nằm trong phần gạch chéo ( kể cả biên ) ở hình vẽ dưới đây thì điều kiện của z là:
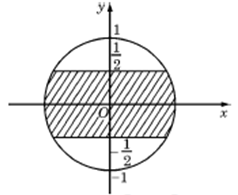
A. \(|z| \le 1\) và phần ảo thuộc đoạn \(\left[ { - \dfrac{1}{2};\dfrac{1}{2}} \right]\).
B. \(|z| \le \dfrac{1}{2}\)và phần thực thuộc đoạn \(\left[ { - \dfrac{1}{2};\dfrac{1}{2}} \right]\).
C. \(|z| \le \dfrac{1}{2}\) và phần ảo thuộc đoạn \(\left[ { - \dfrac{1}{2};\dfrac{1}{2}} \right]\).
D. \(|z| \le 1\) và phần thực thuộc đoạn \(\left[ { - \dfrac{1}{2};\dfrac{1}{2}} \right]\).
Câu 5. Mô đun của số phức z thỏa mãn \(z + \left( {2 + i} \right)\overline z = 3 + 5i\) là:
A. \(\sqrt {17} \) B. \(\sqrt {15} \)
C. \(\sqrt {13} \) D. \(\sqrt {14} \).
Câu 6. Trong tập số phức C, chọn phát biểu đúng .
A. \(z + \overline z \) là số thuần ảo.
B. \(\overline {{z_1} + {z_2}} = \overline {{z_1}} + \overline {{z_2}} \).
C. \({z^2} - {\left( {\overline z } \right)^2} = 4ab\).
D. \(|{z_1} + {z_2}| = |{z_1}| + |{z_2}|\).
Câu 7. Gọi \({z_1}\,,\,{z_2}\) lần lượt là nghiệm của phương trình \({z^2} + 2z + 10 = 0\). Tính \(|{z_1}{|^2} + |{z_2}{|^2}\).
A. 20 B. 50
C. 100 D. 15
Câu 8. Cho số phức z = 2 + 3i. Giá trị của \(|2iz - \overline z |\) bằng :
A. 15 B. \(\sqrt {15} \)
C. 113 D. \(\sqrt {113} \).
Câu 9. Trên mặt phẳng tọa độ, điểm biểu diễn của số phức z = - 5 – 6i là điểm nào sau đây ?
A. P(5 ; - 6). B. Q(5 ; 6).
C. M(- 5 ; 6). D. N(- 5 ; - 6 ).
Câu 10. Tìm số phưc liên hợp của số phức \(z = 1 - 9i\).
A. \(\overline z = - 1 - 9i\).
B. \(\overline z = - 1 + 9i\).
C. \(\overline z = 1 - 9i\).
D. \(\overline z = 1 + 9i\).
Câu 11. Số phức z là số thực nếu:
A. a = 0. B. b = 0.
C. i = 0. D. a. b = 0.
Câu 12. Các số thực x , y thỏa mãn \(\dfrac{{x - 3}}{{3 + i}} + \dfrac{{y - 3}}{{3 - i}} = i\). Khi đó tổng T = x + y bằng :
A. 4 B. 5
C. 6 D. 7
Câu 13. Cho biểu thức \(|z| + z = 3 + 4i\). Số phức z là :
A. \(z = \dfrac{7}{6} - 4i\).
B. \(z = \dfrac{6}{7} + 4i\).
C. \(z = - \dfrac{7}{6} - 4i\).
D. \(z = - \dfrac{7}{6} + 4i\).
Câu 14. Cho số phức z thỏa mãn \(|z - 2 - 2i| = 1\). Số phức z - i có mô đun nhỏ nhất là:
A. \(\sqrt 5 - 1\).
B. \(1 - \sqrt 5 \).
C. \(\sqrt 5 + 1\).
D. \(\sqrt 5 + 2\).
Câu 15. Cho hai số phức \({z_1} = 1 + 2i\,,\,\,{z_2} = 2 - 3i\). Phần thực và phần ảo của số phức \(w = 3{z_1} - 2{z_2}\) là:
A. 1 và 12.
B. – 1 và 12.
C. – 1 và 12i.
D. 1 và 12i.
Câu 16. Cho số phức z thỏa mãn \(|z + 3| + |z - 3| = 10\). Giá trị nhỏ nhất của \(|z|\) là:
A. 3 B. 4
C. 5 D. 6
Câu 17. Nghiệm của phương trình \(2{z^4} + {z^2} - 1 = 0\) trên tập số phức là:
A. \(z = \pm i\).
B. \(\left[ \begin{array}{l}z = \dfrac{{\sqrt 2 }}{2}\\z = i\end{array} \right.\).
C. \(\left[ \begin{array}{l}z = \pm \dfrac{i}{{\sqrt 2 }}\\z = \pm i\end{array} \right.\).
D. \(\left[ \begin{array}{l}z = \pm \dfrac{1}{{\sqrt 2 }}\\z = \pm i\end{array} \right.\).
Câu 18. Tập hợp các điểm biểu diễn số phức z thỏa mãn \(|z| = |2 + 2i|\) là:
A. Đường tròn bán kính \(2\sqrt 2 \).
B. Đường tròn bán kính 4.
C. Đường tròn bán kính 2.
D. Đường tròn bán kính \(4\sqrt 2 \).
Câu 19. Số phức z có mô đun r và acgumen \(\varphi \) thì có dạng lượng giác là:
A. \(z = r\left( {\cos \varphi + i\sin \varphi } \right)\).
B. \(z = r\left( {\cos \varphi - i\sin \varphi } \right)\).
C. \(z = r\left( {\sin \varphi + i\cos \varphi } \right)\).
D. \(z = r\left( {\sin \varphi - i\cos \varphi } \right)\).
Câu 20. Tổng của hai số phức \({z_1} = 1 - 2i\,,\,\,{z_2} = 2 + 3i\) là:
A. \(2 - 5i\).
B. 2 + 5i.
C. 3 + i.
D. 3 + 5i.
Câu 21. Gọi \(\varphi \) là 1 acgumen cảu số phức z có biểu diễn là \(M\left( {\dfrac{1}{2};\dfrac{{\sqrt 3 }}{2}} \right)\)nằm trên đường tròn đơn vị, số đo nào sau đây có thể là một acgumen của z ?
A. \(\dfrac{\pi }{2}\) B. \(\dfrac{\pi }{3}\)
C. \(\dfrac{\pi }{4}\) D. \(\dfrac{\pi }{6}\).
Câu 22. Cho số phức z thỏa mãn \(|z + 1 - i|\,\, \le \,3\)là số thực. Tập hợp điểm M biểu diễn số phức z là:
A. Đường tròn .
B. Đường thẳng .
C. Hình tròn .
D. Một điểm duy nhất.
Câu 23. Cho hai số phức \({z_1} = 4 + 5i\,,\,\,{z_2} = 1 + 2i\). Tìm khẳng định đúng ?
A. \({z_1} + {z_2} = 5 + 7i\).
B. \({z_1} - {z_2} = 3 + 4i\).
C. \({z_1}.{z_2} = 10 + 3i\).
D. \({z_1}.{z_2} = 20 + 5i\).
Câu 24. Tìm điểm M biểu diễn số phức z = 2 + 2i.
A. M ( 2 ; - 2).
B. M (2 ; 2).
C. M ( -2 ; 2).
D. M (-2 ; 2).
Câu 25. Cho số phức z có dạng lượng giác \(z = 4\left( {\cos \left( { - \dfrac{\pi }{2}} \right) + i\sin \left( { - \dfrac{\pi }{2}} \right)} \right)\). Dạng đại số của z là :
A. z = 4.
B. z = - i.
C. z = 4i.
D. z = - 4i.
Câu 1. Cho số phức z thỏa mãn \(2z - \left( {3 + 4i} \right) = 5 - 2i\). Mô đun của z bằng bao nhiêu ?
A. \(\sqrt {15} \). B. 5
C. \(\sqrt {17} \) D. \(\sqrt {29} \).
Câu 2. Cho số phức \(z = {\left( {\dfrac{{1 + 2i}}{{2 - i}}} \right)^{2022}}\). Tìm phát biểu đúng .
A. z là số thuần ảo.
B. z có phần thực âm.
C. z là số thực.
D. z có phần thực dương.
Câu 3. Trong C, cho phương trình bậc hai \(a{z^2} + bz + c = 0\,\,(*)\,\,(a \ne 0)\). Gọi \(\Delta = {b^2} - 4ac\). Ta xét các mệnh đề:
+ Nếu \(\Delta \) là số thực âm thì phương trình (*) vô nghiệm.
+ Nếu \(\Delta \ne 0\) thì phương trình có hai nghiệm số phân biệt.
+ Nếu \(\Delta = 0\) thì phương trình có một nghiệm kép.
Trong các nệnh đề trên:
A. Cả ba mệnh đề đều đúng .
B. Có một mệnh đề đúng.
C. Không mệnh đề nào đúng .
D. Có hai mệnh đề đúng.
Câu 4. Số phức nghịch đảo của số phức \(z = 1 - \sqrt 3 i\) là:
A. \(\dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\).
B. \(1 + \sqrt 3 i\).
C. \(\dfrac{1}{4} + \dfrac{{\sqrt 3 }}{4}i\).
D. \( - 1 + \sqrt 3 i\).
Câu 5. Biết nghịch đảo của số phức z là liên hợp của nó. Chọn mệnh đề đúng
A. \(|z| = 2\)
B. \(|z| = 1\).
C. z là số thực.
D. z là số thuần ảo.
Câu 6. Cho số phức \(z = a + bi\). Tìm mệnh đề đúng.
A. \(z - \overline z = 2a\).
B. \(z + \overline z = 2bi\).
C. \(|{z^2}| = |z{|^2}\).
D. \(z.\overline z = {a^2} + {b^2}\).
Câu 7. Thu gọn số phức \(i\left( {2 - i} \right)\left( {3 + i} \right)\) ta được:
A. 6.
B. 2 + 5i.
C. 1 + 7i.
D. 7i.
Câu 8. Gọi \({z_1}\,,\,{z_2}\) là hai nghiệm của phương trình \({z^2} - 2z + 2 = 0\). Tính giá trị của \(P = \left| {\dfrac{1}{{{z_1}}} + \dfrac{1}{{{z_2}}}} \right|\).
A. P = 1
B. P = 4.
C. P = 0.
D. P = \(\sqrt 2 \).
Câu 9. Cho số phức z = 2 – 3i . Mệnh đề nào sau đây đúng ?
A. Phần thực của z bằng 2 và phần ảo của z bằng 3i.
B. Phần thực của z bằng 2 và phần ảo của z bằng 3.
C. Phần thực của z bằng 2 và phần ảo của z bằng - 3i.
D. Phần thực của z bằng 2 và phần ảo của z bằng - 3.
Câu 10. Tìm b, c \( \in R\) để phương trình \(2{z^2} - bz + c = 0\) có hai nghiệm thuần ảo.
A. \(\left\{ \begin{array}{l}b > 0\\c = 0\end{array} \right.\).
B. \(\left\{ \begin{array}{l}b = 0\\c < 2\end{array} \right.\).
C. \(\left\{ \begin{array}{l}b = 0\\c > - 2\end{array} \right.\).
D. \(\left\{ \begin{array}{l}b = 0\\c > 0\end{array} \right.\).
Câu 11. Hai số phức \(z = a + bi,\,\,z' = a + b'i\) bằng nhau khi:
A. \(a = b'\).
B. a = b .
C. \(b = b'\).
D. a = - b.
Câu 12. Số phức \(z = \dfrac{{3 + 4i}}{{2 + 3i}} + \dfrac{{5 - 2i}}{{2 - 3i}}\) bằng:
A. \(\dfrac{{34}}{{13}} + \dfrac{{10}}{{13}}i\).
B. \(\dfrac{{34}}{{13}} - \dfrac{{10}}{{13}}i\).
C. \( - \dfrac{{34}}{{13}} + \dfrac{{10}}{{13}}i\).
D. \( - \dfrac{{34}}{{13}} - \dfrac{{10}}{{13}}i\).
Câu 13. Cho hai nghiệm \({z_1} = - \sqrt 3 + i\sqrt 2 \,,\,\,{z_2} = - \sqrt 3 - i\sqrt 2 \). Phương trình bậc hai có nghiệm là hai nghiệm trên là:
A. \({z^2} + 3\sqrt 2 z + 5 = 0\).
B. \({z^2} + 2\sqrt 3 z + 5 = 0\).
C. \({z^2} - 2\sqrt 3 z + 5 = 0\).
D. \({z^2} + 5z + 2\sqrt {3 = 0} \).
Câu 14. Cho số phức thỏa mãn điều kiện \(|z - 2 + 2i| = 1\). Tìm giá trị lớn nhất của \(|z|\).
A. \(\max |z| = 2\sqrt 2 + 1\).
B. \(\max |z| = 2\sqrt 2 \).
C. \(\max |z| = 2\sqrt 2 + 2\)
D. \(\max |z| = 2\sqrt 2 - 1\).
Câu 15. Phần thực và phần ảo của số phức \(z = {\left( {1 + \sqrt 3 i} \right)^2}\) là:
A. 1 và 3.
B. 1 và – 3 .
C. – 2 và \(2\sqrt 3 \).
D. 2 và \( - 2\sqrt 3 \).
Câu 16. Cho số phức z có điểm biểu diễn nằm trên đường thẳng 3x – 4y – 3 =0, \(|z|\) nhỏ nhất bằng:
A. \(\dfrac{1}{5}\) B. \(\dfrac{4}{5}\)
C.\(\dfrac{2}{5}\) D. \(\dfrac{3}{5}\).
Câu 17. Mô đun của số phức z thỏa mãn \(\overline z = 8 - 6i\) là:
A. 2 B. 10
C. 14 D. \(2\sqrt 7 \).
Câu 18. Tập hợp các điểm biểu diễn số phức z thỏa mãn \(|z| = 3\) là:
A. Hai đường thẳng .
B. Đường tròn bán kính bằng 3.
C. Đường tròn bán kính bằng 9.
D. Hình tròn bán kính bằng 3.
Câu 19. Cho \(z = r\left( {\cos \varphi + i\sin \varphi } \right)\). Chọn mệnh đề đúng.
A. r là acgumen của z.
B. r là mô đun của z.
C. \(\cos \varphi \) là acgumen của z.
D. \(\sin \varphi \) là acgumen của z.
Câu 20. Tích của hai số phức \({z_1} = 3 + 2i\,,\,\,{z_2} = 2 - 3i\) là;
A. 6 – 6i .
B. 12 + 12i.
C. 12 – 5i.
D. 12 + 5i.
Câu 21. Số phức z có mô đun r = 3 và acgumen \(\varphi = \pi \) thì có dạng lượng giác là:
A. \(z = 3\left( {\cos 2\pi + i\sin 2\pi } \right)\).
B. \(z = 3\left( {\cos \left( { - \pi } \right) + i\sin \left( { - \pi } \right)} \right)\).
C. \(z = 3\left( {\sin \pi + i\cos \pi } \right)\).
D. \(z = 3\left( {{\mathop{\rm s}\nolimits} {\rm{in3}}\pi + i\cos 3\pi } \right)\).
Câu 22. Phương trình \({z^2} + 4z + 13 = 0\)có các nghiệm là;
A. \(2 \pm 3i\).
B. \(4 \pm 6i\).
C. \( - 4 \pm 6i\).
D. \( - 2 \pm 3i\)
Câu 23. Gọi \(\varphi \) là 1 acgumen cảu số phức z có biểu diễn là \(M\left( {\dfrac{{\sqrt 3 }}{2};\dfrac{1}{2}} \right)\)nằm trên đường tròn đơn vị, số đo nào sau đây có thể là một acgumen của z ?
A. \(\dfrac{\pi }{2}\) B. \(\dfrac{\pi }{3}\)
C. \(\dfrac{\pi }{4}\) D. \(\dfrac{\pi }{6}\).
Câu 24. Tìm điểm M biểu diễn số phức z = 3 - 4i.
A. M ( 3 ; - 4). B. M (3 ; 4).
C. M ( -3 ; 4). D. M (-4 ; 3).
Câu 25. Cho số phức z = 6 + 8i. Giá trị của \(S = 2|z| - 1\) bằng bao nhiêu ?
A. S = 10. B. S = 19.
C. S = 11. D. S = 15.
Câu 1. Cho số phức z thỏa mãn \(\overline z = \left( {1 - 3i} \right)\left( { - 2 + i} \right) = 2i\). Tính \(|z|\).
A. \(|z| = 2\).
B. \(|z| = 5\sqrt 2 \).
C. \(|z| = \sqrt {82} \).
D. \(|z| = 4\sqrt 5 \).
Câu 2. Trong mặt phẳng phức, tìm tập hợp điểm M biểu diễn số phức z thỏa mãn \(|z + 1 - i| \le 3\).
A. Hình tròn tâm I(1 ; - 1) , bán kính R = 3.
B. Đường tròn tâm I(-1 ; 1), bán kính R = 9.
C. Hình tròn tâm I(- 1; 1), bán kính R = 3.
D. Đường tròn tâm I(-1 ; 1), bán kính R = 9.
Câu 3. Thu gọn số phức \(z = \dfrac{{3 + 2i}}{{1 - i}} + \dfrac{{1 - i}}{{3 + 2i}}\), ta được:
A. \(z = \dfrac{{15}}{{26}} + \dfrac{{55}}{{26}}i\).
B. \(z = \dfrac{{23}}{{26}} + \dfrac{{63}}{{26}}i\).
C. \(z = \dfrac{2}{{13}} + \dfrac{6}{{13}}i\).
D. \(z = \dfrac{{21}}{{26}} + \dfrac{{61}}{{26}}i\).
Câu 4. Trong mặt phẳng Oxy, tập hợp các điểm biểu diễn cho số phức z thỏa mãn \({z^2}\) là một số ảo là :
A. Trục hoành.
B. Trục tung.
C. Hai đường thẳng \(y = \pm x\)
D. Đường tròn \({x^2} + {y^2} = 1\).
Câu 5. Trong mặt phẳng phức, gọi A, B , C lần lượt là các điểm biểu diễn của các số phức \({z_1} = - 1 + 3i\,,\,\,{z_2} = 1 + 5i\,,\,\,{z_3} = 4 + i\). Số phức z có điểm biểu diễn là điểm D sao cho tứ giác ABCD là hình bình hành là:
A. \(z = 6 + 3i\).
B. \(z = 2 - i\).
C. \(z = 2 + i\).
D. \(z = 6 - 3i\).
Câu 6. Tìm số phức z thỏa mãn \(\left( {3 - 2i} \right)z + \left( {4 + 5i} \right) = 7 + 3i\).
A. \(z = - i\).
B. \(z = - 1\).
C. \(z = i\)
D. \(z = 1\).
Câu 7. Cho hai số phức \(z = a + bi\,,\,\,z' = a' + b'i\). Điều kiện để \(zz'\) là một số thực là :
A. \(ab' + a'b = 0\).
B. \(aa' + bb' = 0\).
C. \(aa' - bb' = 0\).
D. \(ab' - a'b = 0\).
Câu 8. Số phức liên hợp của số phức \(z = - \dfrac{1}{2} + \dfrac{3}{2}i\) là:
A. \(\overline z = \dfrac{3}{2} - \dfrac{1}{2}i\).
B. \(\overline z = - \dfrac{1}{2} - \dfrac{3}{2}i\).
C. \(\overline z = \dfrac{1}{2} - \dfrac{3}{2}i\).
D. \(\overline z = \dfrac{1}{2} + \dfrac{3}{2}i\).
Câu 9. Cho số phức z = 3 + 4i. Giá trị của \(S = 2|z| - 1\) bằng bao nhiêu ?
A. S = 10.
B. S = 9.
C. S = 11.
D. S = 5.
Câu 10. Tìm các số thực x, y thỏa mãn \(\left( {x + 2y} \right) + \left( {2x - 2y} \right)i = 7 - 4i\).
A. \(x = - \dfrac{{11}}{3}\,,\,\,y = \dfrac{1}{3}\).
B. \(x = - 1\,,\,y = - 3\).
C. x = 1, y = 3.
D. \(x = - \dfrac{{11}}{3}\,,\,\,y = - \dfrac{1}{3}\).
Câu 11. Gọi M, N lần lượt là các điểm biểu diễn số phức \(z = a + bi,\,\,z' = a' + b'i\). Chọn câu trả lời đúng.
A. \(M(a;a')\). B. \(N(b;b')\).
C. M(a ; b). D. \(N(a';b')\).
Câu 12. Phần thực và phần ảo của số phức \(z = - \dfrac{{1 + i}}{{1 - i}}\) là:
A. 0 và 1. B. 0 và i.
C. 0 và -1. D. 0 và – i.
Câu 13. Nghiệm của phương trình \(3{z^2} - 4z + 2 = 0\) là:
A. \({z_1} = \dfrac{{ - 2 - i\sqrt 2 }}{3}\,,\,\,{z_2} = \dfrac{{ - 2 + i\sqrt 2 }}{3}\).
B. \({z_1} = \dfrac{{ - 2 - i\sqrt 2 }}{6}\,,\,\,{z_2} = \dfrac{{ - 2 + i\sqrt 2 }}{6}\)
C. \({z_1} = \dfrac{{2 - i\sqrt 2 }}{6}\,,\,\,{z_2} = \dfrac{{2 + i\sqrt 2 }}{6}\).
D. \({z_1} = \dfrac{{2 - i\sqrt 2 }}{3}\,,\,\,{z_2} = \dfrac{{2 + i\sqrt 2 }}{3}\).
Câu 14.Với hai số phức bất kì \({z_1},\,{z_2}\), khẳng định nào sau đây đúng ?
A. \(|{z_1} + {z_2}|\, \le \,|{z_1}| + |{z_2}|\).
B. \(|{z_1} + {z_2}|\, = \,|{z_1}| + |{z_2}|\).
C. \(|{z_1} + {z_2}|\, \ge \,|{z_1}| + |{z_2}|\).
D. \(|{z_1} + {z_2}|\, = \,|{z_1}| + |{z_2}| + |{z_1} - {z_2}|\).
Câu 15. Thực hiện phép tính \(A = \dfrac{{2 + 3i}}{{1 + i}} + \dfrac{{3 - 4i}}{{1 - i}} + i\left( {4 + 9i} \right)\). Ta có:
A. A = 3 + 4i.
B. A = - 3 + 4i.
C. A = 3 - 4i
D. A = - 3 – 4i.
Câu 16. Cho số phức z có \(|z| = 2\) thì số phức \(w = z + 3i\) có mô đun nhỏ nhất và lớn nhất lần lượt là:
A. 2 và 5. B. 1 và 6 .
C. 2 và 6. D. 1 và 5.
Câu 17. Tập hợp các điểm biểu diễn số phức z thỏa mãn \(|z + 3 - 3i| = 5\) là:
A. Đường tròn tâm I(-3 ; 3) bán kính R = 5.
B. Đường tròn tâm I(-3 ; -3) bán kính R = 5.
C. Đường tròn tâm I(3 ; 3) bán kính R = 5.
D. Đường tròn tâm I(3 ; -3) bán kính R = 5.
Câu 18. Gọi \(\varphi \) là một acgumen của z, chọn mệnh đề đúng .
A. \(\varphi + \pi \) là một acgumen của z.
B. \(\varphi - \pi \) là một acgumn của z.
C. \(\varphi - 2\pi \) là một acgumen của z.
D. \(\varphi + 3\pi \) là một acgumen của z.
Câu 19. Số phức \(z = {\left( {1 - i} \right)^3}\) bằng :
A. 1 + i.
B. – 2 – 2i.
C. – 2 + 2i.
D. 4 + 4i.
Câu 20. Nghịch đảo của số phức \(z = 4 + 3i\)là
A. 4 – 3i .
B. \(\dfrac{1}{4} + \dfrac{1}{3}i\).
C. \( - \dfrac{4}{5} + \dfrac{3}{5}i\).
C. \(\dfrac{4}{{25}} - \dfrac{3}{{25}}i\).
Câu 21. Cho A và B là các điểm biểu diễn các số phức \({z_1} = 1 + 2i\,,\,\,{z_2} = 1 - 2i\). Diện tích của tam giác OAB bằng:
A. 1 B. 2
C. 4 D. \(\dfrac{5}{2}\).
Câu 22. Cho số phức z có dạng lượng giác \(z = 4\left( {\cos \left( { - \pi } \right) + i\sin \left( { - \pi } \right)} \right)\). Dạng đại số của z là :
A. z = - 4. B. z = - i.
C. z = 4i. D. z = - 4i.
Câu 23. Cho các số phức \({z_1} = 1 - 4i\,,\,\,{z_2} = - 1 - 3i\). Hãy tính \(|{z_1} + {z_2}|\).
A. 7 B. 10
C. 12 D. 9
Câu 24. Cho số phức \(z = a + bi\). Tìm mệnh đề đúng.
A. \(z - \overline z = 2a\).
B. \(z + \overline z = 2a\).
C. \(|{z^2}| = |z{|^2}\).
D. \(z.\overline z = {a^2} - {b^2}\).
Câu 25. Với hai số phức bất kì \({z_1},\,{z_2}\), khẳng định nào sau đây đúng ?
A. \(|{z_1} + {z_2}|\, = \,|{z_1}| + |{z_2}|\).
B. \(|{z_1} + {z_2}|\, \ge \,|{z_1}| + |{z_2}|\).
C. \(|{z_1} - {z_2}|\,\, \le \,|{z_1}| + |{z_2}|\).
D. \(|{z_1} + {z_2}|\, = \,|{z_1}| + |{z_2}| + |{z_1} - {z_2}|\).
Câu 1. Cho hai số phức \({z_1} = 9 - i,\,\,\,{z_2} = - 3 + 2i\). Tính giá trị của \(\left| {\dfrac{{{z_1}}}{{{z_2}}}} \right|\) bằng bao nhiêu /
A. \(\dfrac{{2\sqrt {154} }}{{13}}\). B. \(\dfrac{{616}}{{169}}\).
C. \(\dfrac{{82}}{{13}}\). D. \(\sqrt {\dfrac{{82}}{{13}}} \).
Câu 2. Cho hai số phức \({z_1} = a + bi,\,\,{z_2} = c + di\)z. Tìm phần thực của số phức \({z_1}.{z_2}\).
A. Phần thực của số phức \({z_1}.{z_2}\) là ac + bd.
B. Phần thực của số phức \({z_1}.{z_2}\) là ac – bd .
C. Phần thực của số phức \({z_1}.{z_2}\) là ad + bc.
D. Phần thực của số phức \({z_1}.{z_2}\) là ad – bc
Câu 3. Cho số phức \(z = - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\). Khi đó số phức \({\left( {\overline z } \right)^2}\) bằng ;
A. \( - \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2}i\).
B. \(\sqrt 3 - i\).
C. \( - \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2}i\).
D. \(1 + \sqrt 3 i\).
Câu 4.Giả sử A, B theo thứ tự là điểm biểu diễn của các số phức \({z_1} = {a_1} + {b_1}i\,,\,\,{z_2} = {a_2} + {b_2}i\). Khi đó độ dài của véc tơ \(\overrightarrow {AB} \) bằng ;
A. \(|{z_1} + {z_2}|\).
B. \(|{z_1}| + |{z_2}|\).
C. \(|{z_1}| - |{z_2}|\).
D. \(|{z_1} - {z_2}|\).
Câu 5. Mô đun của số phức z thỏa mãn \(\dfrac{{2 + i}}{{1 - i}}z = \dfrac{{ - 1 + 3i}}{{2 + i}}\) là:
A. \(\sqrt 5 \) B. \(\dfrac{{\sqrt 5 }}{5}\)
C. \(\dfrac{{2\sqrt 5 }}{5}\) D. \(\dfrac{{3\sqrt 5 }}{5}\).
Câu 6. Tính số phức sau : \(z = {\left( {1 + i} \right)^{15}}\).
A. \(z = - 128 + 128i\).
B. \(z = 128 - 128i\).
C. \(z = 128 + 128i\).
D. \(z = - 128 - 128i\).
Câu 7. Cho số phức z = a + bi. Khi đó số \(\dfrac{1}{2}\left( {z + \overline z } \right)\) là:
A. Một số thuần ảo.
B. 2a.
C. i.
D. a.
Câu 8. Cho các số phức \({z_1} = 2 - 5i\,,\,\,{z_2} = - 2 - 3i\). Hãy tính \(|{z_1} - {z_2}|\).
A. \(2\sqrt 5 \) B. 20
C. 12 D. \(2\sqrt 3 \).
Câu 9. Cho số phức z thỏa mãn \(\left( {3 - 2i} \right)z = 4 + 2i\). Tìm số phức liên hợp của z.
A. \(\overline z = 4 - 2i\).
B. \(\overline z = \dfrac{8}{{13}} + \dfrac{{14}}{{13}}i\).
C. \(\overline z = 3 + 2i\).
D. \(\overline z = \dfrac{8}{{13}} - \dfrac{{14}}{{13}}i\).
Câu 10. Giải phương trình \({z^2} - 6z + 11 = 0\), ta có nghiệm là :
A. \(z = 3 + \sqrt 2 i\).
B. \(z = 3 - \sqrt 2 i\).
C. \(\left[ \begin{array}{l}z = 3 + \sqrt 2 i\\z = 3 - \sqrt 2 i\end{array} \right.\).
D. Một kết quả khác .
Câu 11. Cho hai số phức \(z = a + bi\,,\,\,z' = a' + b'i\). Chọn công thức đúng .
A. \(z + z' = \left( {a + b} \right) + \left( {a' + b'} \right)i\).
B. \(z - z' = \left( {a + a'} \right) - \left( {b + b'} \right)i\).
C. \(z.z' = \left( {aa' - bb'} \right) + \left( {ab' + a'b} \right)i\).
D. \(z.z' = \left( {aa' + bb'} \right) - \left( {ab' + a'b} \right)i\).
Câu 12. Cho z = 1 + 2i. Phần thực và phần ảo của số phức \(w = 2z + \overline z \) là:
A. 3 và 2.
B. 3 và 2i.
C. 1 và 6.
D. 1 và 6i.
Câu 13. Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 1 + i\\3x + iy = 2 - 3i\end{array} \right.\) là:
A. \(\left\{ \begin{array}{l}x = 1 + i\\y = i\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x = i\\y = 1 + i\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x = 1 - i\\y = i\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x = i\\y = 1 - i\end{array} \right.\).
Câu 14. Tìm số phức có phần thực bằng 12 và mô đun bằng 13.
A. \(5 \pm 12i\).
B. 12 + 5i.
C. \(12 \pm 5i\).
D. \(12 \pm i\).
Câu 15. Phương trình \({z^2} - 2z + 3 = 0\) có các nghiệm là:
A. \(2 \pm 2\sqrt 2 i\).
B. \( - 2 \pm 2\sqrt 2 i\).
C. \( - 1 \pm 2\sqrt 2 i\).
D. \(1 \pm \sqrt 2 i\).
Câu 16. Tập hợp các điểm biểu diễn số phức z thỏa mãn \(|\overline z + 3 - 2i| = 4\) là:
A. Đường tròn tâm I(3 ; 2) có bán kính R = 4.
B. Đường tròn tâm I(3 ; -2) có bán kính R= 4.
C. Đường tròn tâm I(-3 ; 2) có bán kính R = 4.
D. Đường tròn tâm I(- 3; -2) có bán kính R = 4.
Câu 17. Hai điểm biểu diễn hai số phức liên hợp \(z = 2 + 2i,\,\,\overline z = 2 - 2i\) đối xứng với nhau qua :
A. Trục tung.
B. Trục hoành.
C. Gốc tọa độ.
D. Điểm A(2; -2).
Câu 18. Cho số phức \(z = r\left( {\cos \dfrac{\pi }{2} + i\sin \dfrac{\pi }{2}} \right)\). Chọn 1 acgumen của z:
A. \( - \dfrac{\pi }{2}\) B. \( - \dfrac{{3\pi }}{2}\)
C. \(\dfrac{{3\pi }}{2}\) D. \(\pi \).
Câu 19. Mô đun của tổng hai số phức \({z_1} = 3 - 4i\,,\,\,{z_2} = 4 + 3i\):
A. \(5\sqrt 2 \) B. 10
C. 8 D. 50.
Câu 20. Cho số phức \(z = - r\left( {\cos \varphi + i\sin \varphi } \right)\). Tìm một acgumen của z ?
A. \( - \varphi \).
B. \(\varphi + 2\pi \).
C. \(\varphi - 2\pi \).
D. \(\varphi + \pi \).
Câu 21. Tính \(z = \dfrac{{5 + 5i}}{{3 - 4i}} + \dfrac{{20}}{{4 + 3i}}\).
A. z = 3 – i.
B. z = 3 + i.
C. z = - 3 – i.
D. z = - 3 + i.
Câu 22.Tập hợp các điểm biểu diễn số phức z thỏa mãn \(|z + 1 + i|\, \le 2\) là;
A. Đường tròn tâm I(1 ; 1) bán kính R = 2.
B. Hình tròn tâm I(1; 1) bán kính R = 2.
C. Đường tròn tâm I(- 1 ; - 1) bán kính R = 2.
D. Hình tròn tâm I(- 1 ; - 1) bán kính R = 2.
Câu 23. Dạng lượng giác của số phức z = i – 1 là:
A. \(z = \sqrt 2 \left( {\cos \dfrac{{3\pi }}{4} - i\sin \dfrac{{3\pi }}{4}} \right)\).
B. \(z = 2\left( {\cos \dfrac{{3\pi }}{4} + i\sin \dfrac{{3\pi }}{4}} \right)\).
C. \(z = \sqrt 2 \left( {\cos \dfrac{{ - \pi }}{4} + i\sin \dfrac{{ - \pi }}{4}} \right)\).
D. \(z = \sqrt 2 \left( {\cos \dfrac{{3\pi }}{4} + i\sin \dfrac{{3\pi }}{4}} \right)\).
Câu 24. Trong mặt phẳng phức, các điểm A, B lần lượt là điểm biểu diễn của \({z_1} = 2 - 4i\,,\,\,{z_2} = 4 + 5i\). Trung điểm của AB có tọa độ là:
A. \(A\left( {3;\dfrac{3}{2}} \right)\).
B. \(A\left( {3;1} \right)\).
C. \(A\left( {3;\dfrac{1}{2}} \right)\).
D. \(A\left( {6;1} \right)\).
Câu 25. Cho số phức z thỏa mãn \(\left( {3 + 2i} \right)z + {\left( {2 - i} \right)^2} = 4 + i\). Mô đun của số phức \(w = \left( {z + 1} \right)\overline z \) là:
A. 2 B. 4
C. 10 D. \(\sqrt {10} \).
Câu 1. Trong mặt phẳng tọa độ Oxy, cho điểm M là điểm biểu diễn cho số phức z = a + bi. Tính S = a + b.
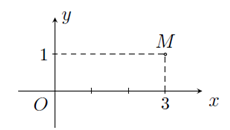
A. S = 4 B. S = 1
C. S = 2 D. S = 3.
Câu 2. Điểm nào trong các điểm sau đây là điểm biểu diễn hình học của số phức z = - 5 + 4i trong mặt phẳng tọa độ Oxy.
A. A(- 5 ; 4). B. B(5 ; - 4 ).
C. C(4 ; - 5). D. D(4 ; 5).
Câu 3. Trong C, phương trình \({z^3} + 1 = 0\) có nghiệm là :
A. \(S = \{ - 1;\,\dfrac{{2 \pm i\sqrt 3 }}{2}\} \).
B. \(S = \{ - 1\} \).
C. \(S = \{ - 1;\dfrac{{5 \pm i\sqrt 3 }}{4}\} \).
D. \(S = \{ - 1;\dfrac{{1 \pm i\sqrt 3 }}{2}\} \).
Câu 4. Số phức z thỏa mãn \(|z| = 5\) và phần thực của z bằng hai lần phần ảo của nó.
A. \(\left[ \begin{array}{l}z = 2\sqrt 5 + i\sqrt 5 \\z = - 2\sqrt 5 - i\sqrt 5 \end{array} \right.\).
B. \(\left[ \begin{array}{l}z = - 2\sqrt 5 + i\sqrt 5 \\z = 2\sqrt 5 - i\sqrt 5 \end{array} \right.\).
C. \(\left[ \begin{array}{l}z = \sqrt 5 + 2\sqrt 5 i\\z = - \sqrt 5 - 2\sqrt 5 i\end{array} \right.\).
D. \(\left[ \begin{array}{l}z = - \sqrt 5 + 2\sqrt 5 i\\z = \sqrt 5 - 2\sqrt 5 i\end{array} \right.\).
Câu 5. Cho số phức z thỏa mãn \(|z - 2 - 2i| = 1\). Tập hợp điểm biểu diễn số phức z – i trong mặt phằng tọa độ là đường tròn có phương trình :
A. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 1\).
B. \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 1\).
C. \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 1\).
D. \({\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 1\)
Câu 6. Điểm biểu diễn cùa các số phức z = 7 + bi với \(b \in R\), nằm trên đường thẳng có phương trình là:
A. x = 7. B. y = 7.
C. y = x. D. y = x + 7.
Câu 7. Gọi A là điểm biểu diễn của số phức z = 2 + 5i và B là điểm biểu diễn của số phức z’ = - 2 +5i. Tìm mệnh đề đúng trong các mệnh để sau:
A. Hai điểm A và B đối xứng với nhau qua đường thẳng y = x.
B. Hai điểm A và B đối xứng với nhau qua trục hoành.
C. Hai điểm A và B đối xứng với nhau qua gốc tọa độ O.
D. Hai điểm A và B đối xứng với nhau qua trục tung.
Câu 8. Biết rằng số phức liên hợp của z là \(\overline z = \left( {2 + 3i} \right) + \left( {4 - 8i} \right)\). Tìm số phức z.
A. \(z = - 6 - 5i\).
B. \(z = 6 + 5i\).
C. \(z = - 6 + 5i\).
D. \(z = 6 - 5i\).
Câu 9. Cho \(\overline z = \left( {5 - 2i} \right)\left( { - 3 + 2i} \right)\). Giá trị của \(2|z| - 5\sqrt {377} \) bằng :
A. \( - 10\sqrt {377} \). B. \(10\sqrt {377} \).
C. \(7\sqrt {377} \). D. \( - 3\sqrt {377} \).
Câu 10. Tìm số phức z biết \(|z| = 5\) và phần thực lớn hơn phần ảo một đơn vị .
A. \({z_1} = 3 + 4i\,,\,\,{z_2} = - 4 - 3i\).
B. \({z_1} = 4 + 3i\,,\,\,{z_2} = - 3 - 4i\).
C. \({z_1} = - 4 - 3i\,,\,\,{z_2} = 3 + 4i\)
D. \({z_1} = \left( {2\sqrt 3 + 1} \right) + 2\sqrt 3 \) \({z_2} = \left( { - 2\sqrt 3 + 1} \right) - 2\sqrt 3 i\)
Câu 11. Cho số phức z = a + bi và \(\overline z \) là số phức liên hợp của z. Chọn kết luận đúng.
A. \(z + \overline z = 2a\). B. \(z.\overline z = 1\).
C. \(z - \overline z = 2b\). D. \(z.\overline z = {z^2}\).
Câu 12. Cho các số phức \({z_1} = - 1 + i\,,\,\,{z_2} = 1 - 2i\,,\,\,{z_3} = 1 + 2i\). Giá trị biểu thức \(T = |{z_1}{z_2} + {z_2}{z_3} + {z_3}{z_1}|\) là:
A. 1 B. \(\sqrt {13} \)
C. 5 D. 13
Câu 13. Cho hai số phức \({z_1} = 3 - 2i\) \({z_2} = \left( {{a^2} + a + 1} \right) + \left( {2{a^2} + 3a - 4} \right)i\). Tìm \(a \in R\) để \({z_1} = {z_2}\).
A. a = -3. B. a = 1.
C. a = - 1 . D. a = - 2 .
Câu 14. Kí hiệu a, b lần lượt là phần thực và phần ảo của số phức \(3 - 2\sqrt 2 i\). Tìm a , b.
A. a = 3 , b = 2.
B. a = 3 , b = \(2\sqrt 2 \).
C. a = 3 , b = \(\sqrt 2 \).
D. a = 3 , b = \( - 2\sqrt 2 \).
Câu 15. Tập hợp các điểm biểu diễn số phức z thỏa mãn \(|z - 2i| = 4\) là:
A. Đường tròn tâm I(1 ; - 2), bán kính R = 4.
B. Đường tròn tâm I(1 ; 2), bán kính R = 4.
C. Đường tròn tâm I(0 ; 2), bán kính R = 4.
D. Đường tròn tâm I(0 ; -2), bán kính R = 4.
Câu 16. Xác định số phức z thỏa mãn \(|z - 2 - 2i| = \sqrt 2 \) mà \(|z|\) đạt giá trị lớn nhất.
A. z = 1 + i.
B. z = 3 + i.
C. z = 3 + 3i.
D. z = 1+ 3i.
Câu 17. Cho số phức \(z = r\left( {\cos \dfrac{\pi }{4} + i\sin \dfrac{\pi }{4}} \right)\). Chọn 1 acgumn của z:
A. \( - \dfrac{\pi }{4}\) B. \(\dfrac{{5\pi }}{4}\)
C. \(\dfrac{{9\pi }}{4}\) D. \( - \dfrac{{5\pi }}{4}\).
Câu 18. Cho số phức \(z = \dfrac{{1 + i}}{{2 - i}}\). Mô đun của z là:
A. \(\sqrt {\dfrac{2}{5}} \). B. \(\sqrt {\dfrac{5}{2}} \)
C. \(\dfrac{2}{5}\) D. \(\dfrac{5}{2}\).
Câu 19. Số phức z có mô đun r = 2 và acgumen \(\varphi = - \dfrac{\pi }{2}\) thì có dạng lượng giác là:
A. \(z = 2\left( {\cos \left( { - \dfrac{\pi }{2}} \right) + i\sin \left( { - \dfrac{\pi }{2}} \right)} \right)\).
B. \(z = 2\left( {\cos \left( { - \dfrac{\pi }{2}} \right) - i\sin \left( { - \dfrac{\pi }{2}} \right)} \right)\).
C. \(z = 2\left( {\cos \left( {\dfrac{\pi }{2}} \right) + i\sin \left( {\dfrac{\pi }{2}} \right)} \right)\).
D. \(z = 2\left( { - \cos \left( { - \dfrac{\pi }{2}} \right) + i\sin \left( { - \dfrac{\pi }{2}} \right)} \right)\).
Câu 20. Phương trình \({z^2} + az + b = 0\) nhận z = 1 – 2i làm nghiệm Khi đó a + b bằng:
A. 3 B. 4
C. 5 D. 6.
Câu 21. Gọi số phức z có dạng đại số và dạng lượng giác lần lượt là z = a + bi và \(z = r\left( {\cos \varphi + i\sin \varphi } \right)\). Chọn mệnh đề đúng .
A. \(r = \sqrt {{a^2} + {b^2}} \).
B. \(r = {a^2} + {b^2}\).
C. \({r^2} = \sqrt {{a^2} + {b^2}} \).
D. \(r = |a + b|\).
Câu 22. Cho số phức z có dạng lượng giác \(z = 2\left( {\cos \dfrac{\pi }{2} + i\sin \dfrac{\pi }{2}} \right)\). Dạng lượng giác của z là:
A. z = 2.
B. z = 2i.
C. z = -2 .
D. z = - 2i.
Câu 23. Trong mặt phẳng phức, A, B, C lần lượt là các điểm biểu diễn của các số phức \({z_1} = 1 + 2i\,,\,\,{z_2} = 2 + 3i\,,\,\,{z_3} = 3 + 4i\). Trọng tâm tam giác ABC là điểm :
A. G ( 2 ; -3 ).
B. G (2 ; 3).
C. G ( 3 ; 2).
D. G (-3 ;2).
Câu 24. Cho số phức z = 4 + 3i. Tìm phần thực và phần ảo của z.
A. Phần thực của z là 4, phần ảo của z là 3.
B. Phần thực của z là 4, phần ảo của z là 3i.
C. Phần thực của z là 3, phần ảo của z là 4.
D. Phần thực của z là 3, phần ảo của z là 4i.
Câu 25. Tổng của hai số phức \({z_1} = 2 + 3i\,,\,\,{z_2} = 5 - 6i\)là:
A. 7 – 3i.
B. 7 + 3i.
C. – 3 +9i.
D. 3 + 9i.
