Nghệ thuật miêu tả tương phản trong Hai đứa trẻ

Tính diện tích hình phẳng giới hạn bởi các đường sau:

a) \(\displaystyle  y = 2x - {x^2},x + y = 2\);

b) \(\displaystyle  y = {x^3} - 12x,y = {x^2}\);

c) \(\displaystyle  x + y = 1;x + y =  - 1;\) \(\displaystyle  x - y = 1;x - y =  - 1\);

d) \(\displaystyle  y = \frac{1}{{1 + {x^2}}},y = \frac{1}{2}\)

e) \(\displaystyle  y = {x^3} - 1\) và tiếp tuyến với \(\displaystyle  y = {x^3} - 1\) tại điểm \(\displaystyle  \left( { - 1; - 2} \right)\).

Tính thể tích vật thể:

a) Có đáy là một tam giác cho bởi: \(\displaystyle  y = x,y = 0\), và \(\displaystyle  x = 1\). Mỗi thiết diện vuông góc với trục \(\displaystyle  Ox\) là một hình vuông.

b) Có đáy là một hình tròn giới hạn bởi \(\displaystyle  {x^2} + {y^2} = 1\). Mỗi thiết diện vuông góc với trục \(\displaystyle  Ox\) là một hình vuông.

Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi:

a) \(\displaystyle  y = 2 - {x^2},y = 1\), quanh trục \(\displaystyle  Ox\).

b) \(\displaystyle  y = 2x - {x^2},y = x\), quanh trục \(\displaystyle  Ox\).

c) \(\displaystyle  y = {(2x + 1)^{\frac{1}{3}}},x = 0,y = 3\), quanh trục \(\displaystyle  Oy\).

Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục \(\displaystyle  Ox\) hình phẳng giới hạn bởi các đường \(\displaystyle  y = \frac{1}{x}\), \(\displaystyle  y = 0,x = 1\) và \(\displaystyle  x = a\left( {a > 1} \right)\). Gọi thể tích đó là \(\displaystyle  V\left( a \right)\). Xác định thể tích của vật thể khi \(\displaystyle  a \to  + \infty \) (tức là \(\displaystyle  \mathop {\lim }\limits_{a \to  + \infty } V(a)\)).

Một hình phẳng được giới hạn bởi \(\displaystyle  y = {e^{ - x}},y = 0,x = 0,x = 1\). Ta chia đoạn \(\displaystyle  \left[ {0;1} \right]\) thành \(\displaystyle  n\) phần bằng nhau tạo thành một hình bậc thang (bởi \(\displaystyle  n\) hình chữ nhật con như dưới).

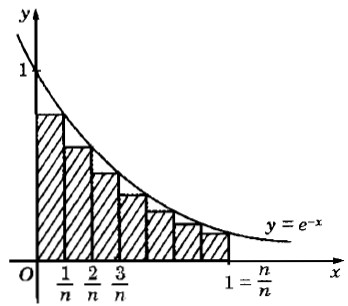
a) Tính diện tích \(\displaystyle  {S_n}\) của hình bậc thang (tổng diện tích của \(\displaystyle  n\) hình chữ nhật con).

b) Tìm \(\displaystyle  \mathop {\lim }\limits_{n \to \infty } {S_n}\) và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân.

Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?

a) \(\displaystyle  {\rm{\{ }}y = x + \sin x,y = x\)  với \(\displaystyle  0 \le x \le \pi {\rm{\} }}\) và \(\displaystyle  {\rm{\{ }}y = x + \sin x,y = x\)  với \(\displaystyle  \pi  \le x \le 2\pi {\rm{\} }}\)

b) \(\displaystyle  \;{\rm{\{ }}y = \sin x,y = 0\) với \(\displaystyle  0 \le x \le \pi {\rm{\} }}\) và \(\displaystyle  {\rm{\{ }}y = \cos x,y = 0\)  với \(\displaystyle  0 \le x \le \pi {\rm{\} }}\);

c) \(\displaystyle  {\rm{\{ }}y = \sqrt x ,y = {x^2}{\rm{\} }}\) và \(\displaystyle  {\rm{\{ }}y = \sqrt {1 - {x^2}} ,y = 1 - x{\rm{\} }}\)

Cho hình phẳng \(\displaystyle  R\) giới hạn bởi các đường sau đây: \(\displaystyle  {y_1} = {f_1}\left( x \right).{y_2} = {f_2}\left( x \right)\) (\(\displaystyle  {f_1},{f_2}\) là các hàm số liên tục trên đoạn \(\displaystyle  \left[ {a;b} \right]\)), \(\displaystyle  x = a\) và \(\displaystyle  x = b\). Hãy chỉ ra công thức sai trong việc tính diện tích hình \(\displaystyle  R\).

A. \(\displaystyle  \int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} \)

B. \(\displaystyle  \int\limits_a^b {\left| {{f_2}\left( x \right) - {f_1}\left( x \right)} \right|dx} \)

C. \(\displaystyle  \left| {\int\limits_a^b {\left| {{f_1}\left( x \right) - {f_2}\left( x \right)} \right|dx} } \right|\)

D. \(\displaystyle  \left| {\int\limits_a^b {\left[ {{f_1}\left( x \right) - {f_2}\left( x \right)} \right]dx} } \right|\)

Diện tích hình phẳng \(\displaystyle  P\) giới hạn bởi các đường \(\displaystyle  {y_1} = x,{y_2} = 2x,{y_3} = 2 - x\) bằng:

A. \(\displaystyle  1\)                       B. \(\displaystyle  \frac{2}{3}\)

C. \(\displaystyle  2\)                       D. \(\displaystyle  \frac{1}{3}\)

Diện tích của hình phẳng giới hạn bởi các đường \(\displaystyle  {y_1} = {x^3};{y_2} = 4x\) bằng

A. \(\displaystyle  0\)                   B. \(\displaystyle  4\)

C. \(\displaystyle  8\)                   D. \(\displaystyle   - 8\)

Cho hình phẳng \(\displaystyle  H\) giới hạn bởi các đường \(\displaystyle  y = f\left( x \right)\), \(\displaystyle  y = 0\), \(\displaystyle  x = b\) và \(\displaystyle  x = a\) (trong đó hàm số \(\displaystyle  f\left( x \right)\) liên tục trên đoạn \(\displaystyle  \left[ {b;a} \right]\)). Thể tích khối tròn xoay tạo nên bởi phép quay hình \(\displaystyle  H\) quanh trục \(\displaystyle  Ox\) được cho bởi công thức:

A. \(\displaystyle  \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)   

B. \(\displaystyle  \int\limits_a^b {{f^2}\left( x \right)dx} \)

C. \(\displaystyle  \pi \int\limits_b^a {{f^2}\left( x \right)dx} \)   

D. \(\displaystyle  \int\limits_a^b {{{\left[ {\pi f\left( x \right)} \right]}^2}dx} \)

Quay hình phẳng \(\displaystyle  Q\) giới hạn bởi các đường \(\displaystyle  {y_1} = \sin x\) và \(\displaystyle  {y_2} = \frac{{2x}}{\pi }\) quanh trục \(\displaystyle  Ox\), ta được một khối tròn xoay. Khi đó thể tích của khối tròn xoay này bằng

A. \(\displaystyle  \frac{1}{6}\)                    B. \(\displaystyle  \frac{\pi }{6}\)

C. \(\displaystyle  8\)                      D. \(\displaystyle  \frac{{{\pi ^2}}}{6}\)

Quay hình phẳng \(\displaystyle  G\) giới hạn bởi các đường \(\displaystyle  y = {x^3},y = 1,x = 0\) xung quanh trục \(\displaystyle  Oy\). Khi đó thể tích của khối tròn xoay này bằng:

A. \(\displaystyle  \pi \)                   B. \(\displaystyle  \frac{5}{3}\pi \)

C. \(\displaystyle  \frac{3}{5}\pi \)                D. \(\displaystyle  \frac{3}{5}\)