Nhân vật Mị trong truyện Vợ chồng A Phủ là một thành công của Tô Hoài trong việc xây dựng con người thức tỉnh. Hãy chứng minh nhận định ấy

Câu I  Cho hai biểu thức :

\(P = \dfrac{{a - 9}}{{\sqrt a  - 3}}\) và \(Q = \dfrac{3}{{\sqrt a  - 3}} + \dfrac{2}{{\sqrt a  + 3}}\)\(\, + \dfrac{{a - 5\sqrt a  - 3}}{{a - 9}}\)  với \(a \ge 0,a \ne 9\)

1) Khi \(a = 81\), tính giá trị biểu thức P .

2) Rút gọn biểu thức Q .

3) Với \(a > 9\), tìm giá trị nhỏ nhất của biểu thức \(A = P.Q\)

Câu II   Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình :

Hai đội công nhân làm chung một công việc và dự định 12 ngày thì hoàn thành xong. Nhưng khi làm chung được 8 ngày, thì đội I được điều động đi làm việc khác. Đội II tiếp tục làm nốt phần việc còn lại. Khi làm một mình, do cải tiến cách làm, năng suất cảu đội II tăng gấp đôi, nên đội II đẫ hoàn thành xong phần việc còn lại trong 3,5 ngày. Hỏi với năng suất ban đầu, nếu mỗi đội làm mọt mình thì sau thời gian bao lâu sẽ hoàn thành công việc trên ?

Câu III 

1) Giải hệ phương trình :\(\left\{ {_{\dfrac{2}{{x - 2}} - \dfrac{3}{{y - 1}} = 1}^{\dfrac{1}{{x - 2}} + \dfrac{1}{{y - 1}} = 2}} \right.\)

2) Cho parabol \((P):y = {x^2}\) và đương thẳng \((d):y = (2m + 1)x - 2m\)

     (\(x\) là ẩn, \(m\) là tham số )

a) Khi m=1. Xác định tọa độ giao điểm của \((d)\) và \((P)\) .

b) Tìm m để \((d)\) và \((P)\) cắt nhau tại hai điểm phân biệt\(A({x_1};{y_1});B({x_2};{y_2})\)

Sao cho biểu thức \(T = x_1^2 + x_2^2 - {x_1}{x_2}\) đạt giá trị nhỏ nhất.

Câu IV: Từ một điểm A nằm ngoài đường tròn \((O;R)\) vẽ tiếp tuyến AB, AC với đường tròn (BC là tiếp điểm). Trên cung nhỏ BC lấy một điểm M bất kỳ, vẽ MI vuông góc với AB, MK vuông góc với AC\((I \in AB,K \in AC)\)

a) Chứng minh : tứ giác\(AIMK\)nội tiếp đường tròn

b) Vẽ  vuông góc với \(BC\left( {P \in BC} \right)\) . Chứng minh : \(\widehat {MPK} = \widehat {MBC}\)

c) Chứng minh rằng : \(MI.MK = M{P^2}\)

d) Xác định vị trí của điểm M trên cung nhỏ BC để tích \(MI.MK.MP\) đạt giá trị lớn nhất.

Câu V Cho ba số \(x,y,z\) không âm và \({x^2} + {y^2} + {z^2} \le 3y\)

Tìm giá trị nhỏ nhất của \(P = \dfrac{1}{{{{(x + 1)}^2}}} + \dfrac{4}{{{{(y + 2)}^2}}} + \dfrac{8}{{{{(z + 3)}^2}}}\)

Bài I  Cho hai biểu thức  \(A = \dfrac{{\sqrt x  + 2}}{{1 + \sqrt x }}\)và \(B = \left( {\dfrac{{2\sqrt x }}{{x - \sqrt x  - 6}} + \dfrac{{\sqrt x }}{{\sqrt x  - 3}}} \right)\)\(\,:\dfrac{{\sqrt x }}{{\sqrt x  - 3}}\)

   với  \(x > 0,x \ne 9.\)

1) Tính giá trị biểu thức \(A\) khi \(x = 36.\)

2) Rút gọn biểu thức  \(B.\)

3) Với \(x \in {\bf{Z}},\) tìm giá trị lớn nhất của biểu thức \(P = AB.\)

Bài II . Giải bài toán sau bằng cách lập hệ phương trình:           

Theo kế hoạch, hai xí nghiệp A và B phải làm tổng cộng 720 dụng cụ cùng loại. Trên thực tế do cải tiến kĩ thuật, xí nghiệp A hoàn thành vượt mức 12%, còn xí nghiệp B hoàn thành vượt mức 10% so với kế hoạch. Do đó thực tế cả hai xí nghiệp làm được tổng cộng 800 dụng cụ. Tính số dụng cụ mỗi xí nghiệp phải làm theo kế hoạch?

Bài III 

1) Giải phương trình :   \(3{x^4} - 2{x^2} - 40 = 0\)

2) Cho phương trình \({x^2} + \left( {m - 1} \right)x - {m^2} - 2 = 0\,\,\,\,(1),\) với \(m\) là tham số thực.

 a) Chứng minh: phương trình (1) luôn có hai nghiệm trái dấu \({x_1},{x_2}\) với mọi giá trị của \(m\).

 b) Tìm \(m\) để biểu thức \(T = {\left( {\dfrac{{{x_1}}}{{{x_2}}}} \right)^3} + {\left( {\dfrac{{{x_2}}}{{{x_1}}}} \right)^3}\) đạt giá trị lớn nhất.

Bài IV .

Cho tam giác \(ABC\) nhọn, nội tiếp đường tròn \(\left( O \right).\) Ba đường cao \(AD,\,BE,\,CF\) của tam giác \(ABC\) cùng đi qua trực tâm \(H.\)

1) Chứng minh: Tứ giác \(BFEC\) nội tiếp.

2) Kẻ đường kính \(AK\) của đường tròn \(\left( O \right).\)

Chứng minh: tam giác \(ABD\) đồng dạng với tam giác \(AKC\) và \(AB.AC = 2AD.R.\)

3) Gọi \(M\) là hình chiếu vuông góc của \(C\) trên \(AK.\) Chứng minh: \(MD\) song song với \(BK.\)

4) Giả sử \(BC\) là dây cố định của đường tròn \(\left( O \right)\) còn \(A\) di động trên cung lớn \(BC.\) Tìm vị trí     của điểm \(A\) để diện tích tam giác \(AEH\) lớn nhất.

Bài V .

Cho \(a,b,c\) là các số thực dương thỏa mãn: \(ab + bc + ac = 3abc.\)Tìm giá trị nhỏ nhất của biểu thức:

\(K = \dfrac{{{a^2}}}{{c\left( {{c^2} + {a^2}} \right)}} + \dfrac{{{b^2}}}{{a\left( {{a^2} + {b^2}} \right)}} \)\(\,+ \dfrac{{{c^2}}}{{b\left( {{b^2} + {c^2}} \right)}}\,.\)

Bài I:  Cho biểu thức \(P = \dfrac{1}{{x - 2\sqrt x }} - \dfrac{2}{{x - 4}}\) với \(x \ne 4,x > 0\)

1) Rút gọn biểu thức P

2) Chứng minh rằng P < 0 với mọi \(x \ne 4,x > 0\)

3) Tìm những giá trị của x để \(P =  - \dfrac{1}{{15}}\)

Bài II: Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình

Một người đi ô tô từ A đến B cách nhau 90km. Khi đi từ B trở về A người đó tăng tốc độ 5km/h so với lúc đi, vì vậy thời gian về ít hơn thời gian đi là 15 phút. Tính tốc độ của ô tô lúc đi từ A đến B.

Bài III: 

1) Giải hệ phương trình \(\left\{ \begin{array}{l}\dfrac{{108}}{x} - \dfrac{{63}}{y} = 7\\\dfrac{{81}}{x} - \dfrac{{84}}{y} = 7\end{array} \right.\)

2) Cho đường thẳng \(\left( d \right):y = \dfrac{{ - 1}}{2}x + 2\) và Parabol \(\left( P \right):y = \dfrac{1}{4}{x^2}\) trên hệ trục tọa độ Oxy.

a) Vẽ parabol (P) và đường thẳng (d) đã cho.

b) Gọi A, B là hai giao điểm của (d) và (P). Tìm điểm N trên trục hoành sao cho tam giác NAB cân tại N.

Bài IV: 

Cho đường tròn (O; R) và dây BC cố định, \(BC = R\sqrt 3 .\) A là điểm di động trên cung lớn BC (A khác B, C) sao cho tam giác ABC nhọn. Các đường cao BD và CE của tam giác ABC cắt nhau tại điểm H. Kẻ đường kính AF của đường tròn (O), AF cắt BC tại điểm N.

a) Chứng minh tứ giác BEDC là tứ giác nội tiếp

b) Chứng minh AE.AB = AD.AC

c) Chứng minh tứ giác BHCF là hình bình hành

d) Đường tròn ngoại tiếp tam giác ADE cắt đường tròn (O) tại điểm thứ hai K (K khác O). Chứng minh ba điểm K, H, F thẳng hàng.

Bài V: 

Cho hai số thực m và n khác 0 thỏa mãn \(\dfrac{1}{m} + \dfrac{1}{n} = \dfrac{1}{2}.\) Chứng minh rằng trong hai phương trình \({x^2} + mx + n = 0\) và \({x^2} + nx + m = 0\) có ít nhất một phương trình có nghiệm.

Bài I : Cho hai biểu thức \(A = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 1}}\) và \(B = \left( {\dfrac{1}{{\sqrt x  - 1}} + \dfrac{{\sqrt x }}{{x - 1}}} \right).\dfrac{{x - \sqrt x }}{{2\sqrt x  + 1}}\) với \(x \ge 0\) và \(x \ne 1\)

1) Tính giá trị của A khi \(x = \dfrac{9}{4}\)

2) Rút gọn B

3) Với \(x \in \mathbb{N}\) và \(x \ne 1\), hãy tìm giá trị lớn nhất của biểu thức \(P = A.B\)

Bài II : Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình

Nhà bạn Mai có một mảnh vườn, được chia thành nhiều luống, mỗi luống trồng số lượng cây bắp cải như nhau. Mai tính rằng nếu tăng thêm 7 luống nhưng mỗi luống trồng ít đi 2 cây thì số lượng cây bắp cải toàn vườn giảm 9 cây; còn nếu giảm đi 5 luống nhưng mỗi luống trồng tăng thêm 2 cây thì số cải bắp cải toàn vườn sẽ tăng thêm 15 cây. Hỏi vườn nhà Mai hiện trồng tổng cộng bao nhiêu cây bắp cải?

Bài III:

1) Giải hệ phương trình \(\left\{ \begin{array}{l}\dfrac{9}{{\sqrt {2x - 1} }} - \dfrac{3}{{y + 1}} = 2\\\dfrac{4}{{\sqrt {2x - 1} }} - \dfrac{1}{{y + 1}} = 1\end{array} \right.\)

2) Cho đường thẳng \(d:y = 2x + {m^2} - 1\) và parabol \(\left( P \right):y = {x^2}\) (với m là tham số) trong mặt phẳng tọa độ Oxy

a) Tìm m để d cắt (P) tại hai điểm phân biệt A và B

Gọi H và K lần lượt là hình chiếu vuông góc của A và B trên trục hoành.Tìm m để độ dài đoạn thẳngHK bằng 3 (đơn vị độ dài)

Bài IV : Cho nửa đường tròn (O) đường kính \(AB = 2R;\) C là điểm bất kì nằm trên nửa đường tròn sao cho C khác A và \(AC < CB.\) Điểm D thuộc cung nhỏ BC sao cho \(\widehat {COD} = {90^0}.\) Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD.

1) Chứng minh CEDF là tứ giác nội tiếp

2) Chứng minh FC.FA = FD.FB

3) Gọi I là trung điểm của EF. Chứng minh IC là tiếp tuyến của (O)

4) Hỏi khi C thay đổi thỏa mãn điều kiện bài toán, E thuộc đường tròn cố định nào?

Bài V : Cho hai số thực dương x và y thỏa mãn \(\dfrac{x}{2} + \dfrac{y}{8} \le 2.\) Tìm giá trị nhỏ nhất của biểu thức \(K = \dfrac{x}{y} + \dfrac{{2y}}{x}\)

Bài I: 

Cho các biểu thức \(P = \dfrac{{\sqrt x  + 3}}{{\sqrt x  - 2}}\)\(\, + \dfrac{{\sqrt x  + 2}}{{3 - \sqrt x }} + \dfrac{{\sqrt x  + 2}}{{x - 5\sqrt x  + 6}}\) và \(Q = 1 - \dfrac{{\sqrt x }}{{\sqrt x  + 1}}\) với \(x \ge 0;x \ne 4;x \ne 9\)

a) Tính giá trị của biểu thức Q khi \(x = 4 + 2\sqrt 3 \)

b) Rút gọn biểu thức \(T = P:Q\)

c) Tìm x để \(\dfrac{1}{T}\) có giá trị nguyên

Câu II:  Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình

Bạn An dự định thực hiện công việc quét sơn cho \(40{m^2}\) tường trong một thời gian nhất định. Tuy nhiên, khi thực hiện mỗi giờ bạn An quét được ít hơn dự định là \(2{m^2}\), do đó bạn đã hoàn thành công việc chậm hơn so với kế hoạch là một giờ. Hỏi nếu đúng kế hoạch thì bạn An hoàn thành công việc trong bao lâu?

Câu III: 

1) Giải hệ phương trình \(\left\{ \begin{array}{l}\dfrac{1}{{2x - y}} + x + 3y = \dfrac{3}{2}\\\dfrac{4}{{2x - y}} - 5\left( {x + 3y} \right) =  - 3\end{array} \right.\)

2) Trong mặt phẳng tọa độ Oxy cho đường thẳng \(\left( d \right):y = mx - 2m + 3\) và parabol \(\left( P \right):y = {x^2}\)

a) Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ \({x_1},\) \({x_2}\) thỏa mãn \(x_1^2{x_2} + x_2^2{x_1} = 5\)

b) Tìm giá trị nguyên nhỏ nhất của m để (d) và (P) không có điểm chung.

Câu IV:  Cho tam giác ABC nội tiếp đường tròn (O). Các đường cao BE và CF cắt nhau tại H.

1) Chứng minh tứ giác BFEC là tứ giác nội tiếp

2) Chứng minh \(AF.AB = AE.AC\)

3) BE và CF lần lượt cắt (O) tại điểm thứ hai là M và N. Chứng minh EF // MN

4) Giả sử B và C cố định; A thay đổi. Tìm vị trị của A sao cho tam giác AEH có diện tích lớn nhất.

Câu V:  Với các số dương x, y, z, t thỏa mãn \(x + y + z + t = 4.\) Tìm giá trị nhỏ nhất của biểu thức \(A = \dfrac{1}{{{x^2} + 1}} + \dfrac{1}{{{y^2} + 1}} + \dfrac{1}{{{z^2} + 1}} \)\(\,+ \dfrac{1}{{{t^2} + 1}}\).

+ Giải đúng pt được: \(x =  - 8\) (không thỏa mãn), \(x = 10\) (thỏa mãn)

+ Kết luận thời gian dự định hoàn thành công việc là 4 giờ

Bài III:

1)

ĐKXĐ: \(2x \ne y\)

Đặt \(\dfrac{1}{{2x - y}} = a;x + 3y = b\)

Ta có hệ: \(\left\{ \begin{array}{l}a + b = \dfrac{3}{2}\\4a - 5b =  - 3\end{array} \right.\)

Giải hệ tìm được \(a = \dfrac{1}{2};b = 1\)

Giải hệ \(\left\{ \begin{array}{l}2x - y = 2\\x + 3y = 1\end{array} \right.\) tìm được \(x = 1;y = 0(TM)\)

2) 

a)

+ Xét phương trình hoành độ giao điểm của (P) và (d)

\(\begin{array}{l}{x^2} = mx - 2m + 3(1)\\ \Leftrightarrow {x^2} - mx + 2m - 3 = 0\end{array}\)

\(\Delta  = {m^2} - 8m + 12 = {\left( {m - 4} \right)^2} - 4\)

(P) cắt (d) tại hai điểm phân biệt khi (1) có hai nghiệm phân biệt khi và chỉ khi \(\Delta  > 0\)

\(\begin{array}{l}\Delta  > 0 \Leftrightarrow {\left( {m - 4} \right)^2} > 4\\ \Leftrightarrow \left[ \begin{array}{l}m - 4 > 2\\m - 4 <  - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > 6\\m < 2\end{array} \right.\end{array}\)

+ Với m > 6 hoặc m < 2, (P) cắt (d) tại hai điểm phân biệt \({x_1},{x_2}\) là nghiệm của pt (1)

Theo Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}.{x_2} = 2m - 3\end{array} \right.\)

\(x_1^2{x_2} + x_2^2{x_1} = 5 \)

\(\Leftrightarrow {x_1}{x_2}\left( {{x_1} + {x_2}} \right) = 5\)

\(\Leftrightarrow m(2m - 3) = 5\)

\(\Leftrightarrow 2{m^2} - 3m - 5 = 0\)

Tìm được \(m =  - 1(TM)\) và \(m = \dfrac{5}{2}(KTM)\)

Vậy \(m=-1\) thỏa mãn yêu cầu bài toán.

b)

(P) và (d) không có điểm chung khi pt (1) vô nghiệm

\(\Delta  < 0 \Leftrightarrow {\left( {m - 4} \right)^2} - 4 < 0\)

\(\Leftrightarrow {\left( {m - 4} \right)^2} < 4\)

\(\Leftrightarrow 2 < m < 6\)

Mà m là số nguyên nên \(m \in \left\{ {3;4;5} \right\}\)

Vậy giá trị m nguyên nhỏ nhất để d không cắt (P) là m = 3

Bài IV:

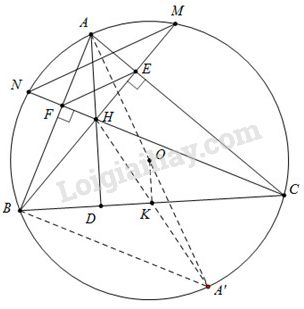
a) Chứng minh được tứ giác BFEC nội tiếp đường tròn đường kính BC

b) Chứng minh được \(\Delta AHF\) đồng dạng với \(\Delta ABD\)

\( \Rightarrow AF.AB = AH.AD\) (1)

Chứng minh \(\Delta AEH\) đồgn dạng với \(\Delta ADC\)

Suy ra \(AE.AC = AH.AD\) (2)

(1) và (2) suy ra AF.AB = AE.AC

(Hoặc chứng minh \(\Delta AEF\) đồng dạng với \(\Delta ABC\))

c)

+ Chứng minh được \(\widehat {MAC} = \widehat {CAD}\) hay \(\widehat {MAE} = \widehat {EAH}\) suy ra AE là trung trực của HM, suy ra E là trung điểm của HM

+ Tương tự chứng minh được F là trung điểm của HN

Suy ra FE // MN (đường trung bình)

(Hoặc có thể chứng minh \(\widehat {FCB} = \widehat {FEB} = \widehat {NMB}\))

d) \(4{S_{\Delta AEH}} = 2AE.EH \le A{E^2} + E{H^2} \)\(\,= A{H^2}\)

Chứng minh AH = 2OK, OK không đổi.

Lập luận, kết luận được \({S_{\Delta AEH}}\) lớn nhất khi AE = EH hay \(\widehat {HAE} = {45^0} \Rightarrow \widehat {ACB} = {45^0},\) suy ra vị trí A

Bài V:

Với các số dương x, y, z, t

Biến đổi và áp dụng bất đẳng thức Cô si chứng minh được:

\(\dfrac{1}{{{x^2} + 1}} = 1 - \dfrac{{{x^2}}}{{{x^2} + 1}} \ge 1 - \dfrac{x}{2};\)

Dấu "=" xảy ra \( \Leftrightarrow x = 1\)

Chứng minh tương tự:

\(\dfrac{1}{{{y^2} + 1}} = 1 - \dfrac{{{y^2}}}{{{y^2} + 1}} \ge 1 - \dfrac{y}{2};\)

Dấu "=" xảy ra \( \Leftrightarrow y = 1\)

\(\dfrac{1}{{{z^2} + 1}} = 1 - \dfrac{{{z^2}}}{{{z^2} + 1}} \ge 1 - \dfrac{z}{2};\)

Dấu "=" xảy ra \( \Leftrightarrow z = 1\)

\(\dfrac{1}{{{t^2} + 1}} = 1 - \dfrac{{{t^2}}}{{{t^2} + 1}} \ge 1 - \dfrac{t}{2};\)

Dấu "=" xảy ra \( \Leftrightarrow t = 1\)

Mà \(x + y + z + t = 4\)

Do đó \(A = \dfrac{1}{{{x^2} + 1}} + \dfrac{1}{{{y^2} + 1}} + \dfrac{1}{{{z^2} + 1}} \)\(\,+ \dfrac{1}{{{t^2} + 1}} \ge 2\)

Vậy giá trị nhỏ nhất của A là 2 \( \Leftrightarrow x = y = z = t = 1\)

Câu I: 

Cho hai biểu thức \(A = \dfrac{{\sqrt x }}{{1 + 3\sqrt x }}\) và \(B = \dfrac{{x + 3}}{{x - 9}} + \dfrac{2}{{\sqrt x  + 3}} - \dfrac{1}{{3 - \sqrt x }}\) với \(x \ge 0;x \ne 9\)

a) Tính giá trị của biểu thức A khi \(x = \dfrac{4}{9}\)

b) Rút gọn biểu thức B

c) Cho \(P = B:A.\) Tìm x để P < 3.

Câu II:  Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình

Hai công nhân cùng làm chung một công việc thì trong 8 giờ xong việc. Nếu mỗi người làm một mình, để hoàn thành công việc đó thì người thứ nhất cần nhiều hơn người thứ hai là 12 giờ. Hỏi nếu làm một mình thì mỗi người phải làm trong bao nhiêu giờ xong công việc đó?

Câu III: 

1) Giải hệ phương trình \(\left\{ \begin{array}{l}\dfrac{1}{{2x - 1}} + \dfrac{4}{{y + 5}} = 3\\\dfrac{3}{{2x - 1}} - \dfrac{2}{{y + 5}} =  - 5\end{array} \right.\)

2) Cho phương trình \({x^2} - 2(m + 1)x + 2m = 0\) (1) (x là ẩn số, m là tham số)

a) Chứng minh phương trình (1) luôn có hai nghiệm phân biệt với mọi m

b) Gọi hai nghiệm của phương trình (1) là \({x_1},\) \({x_2}\). Tìm giá trị của m để \({x_1},\) \({x_2}\) là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng \(\sqrt {12} \).

Câu IV:  Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E bất kỳ (E khác A và C). Kẻ CK vuông góc với AE tại K. Đường thẳng DE cắt CK tại F.

a) Chứng minh tứ giác AHCK là tứ giác nội tiếp

b) Chứng minh KH song song với ED và tam giác ACF là tam giác cân.

c) Tìm vị trí của điểm E để diện tích tam giác ADF lớn nhất.

Câu V:  Giải phương trình \(\sqrt {5{x^2} + 4x}  - \sqrt {{x^2} - 3x - 18}  = 5\sqrt x \)

I. TRẮC NGHIỆM . 

Câu 1. Cặp số \(\left( { - 1;2} \right)\) là nghiệm của hệ phương trình nào sau đây?

A.\(\left\{ \begin{array}{l}x + 5y = 9\\6x + 2y =  - 2\end{array} \right.\)

B. \(\left\{ \begin{array}{l} - 2x + y = 7\\x - \dfrac{3}{4}y = 3\end{array} \right.\)

C. \(\left\{ \begin{array}{l}x + y = 1\\ - 2x + y = 4\end{array} \right.\)

D. \(\left\{ \begin{array}{l}2x - 2y = 0\\x + y = 3\end{array} \right.\)

Câu 2. Điều kiện của m để phương trình \({x^2} - 2mx + {m^2} - 4 = 0\) có hai nghiệm \({x_1} = 0,{x_2} > 0\) là:

A. \(m =  - 2\)

B. \(m = 2\)

C. \(m =  \pm 2\)

D. \(m = 16\)

Câu 3. Cho đường tròn \(\left( {O,R} \right)\) đường kính AB, dây \(AC = R\). Khi đó số đo độ của cung nhỏ BC là:

A.\({60^0}\)                 B. \({120^0}\)

C. \({90^0}\)                D. \({150^0}\)

Câu 4. Độ dài của một đường tròn là \(10\pi \) (cm). Diện tích của hình tròn đó là:

A. \(10\pi \left( {c{m^2}} \right)\)

B. \(100\pi \left( {c{m^2}} \right)\)

C. \(50\pi \left( {c{m^2}} \right)\)

D. \(25\pi \left( {c{m^2}} \right)\)

II. TỰ LUẬN 

Bài I 

1. Giải hệ phương trình sau: \(\left\{ {\begin{array}{*{20}{c}}{\dfrac{2}{{x - 2}} + \dfrac{1}{{y + 1}} = 3}\\{\dfrac{3}{{x - 2}} - \dfrac{2}{{y + 1}} = 8}\end{array}} \right.\) 

2. Trong mặt phẳng tọa độ \({\rm{O}}xy\) cho Parabol (P) : \(y = {x^2}\) và đường thẳng (d) : \(y = 2mx - 2m + 1\)

a) Với \(m =  - 1\) . Hãy tìm tọa độ giao điểm của (P) và (d) .

b) Tìm m để (d) và (P) cắt nhau tại 2 điểm phân biệt  : \(A({x_1};{y_2});B({x_2};{y_2})\) sao cho tổng các tung độ của hai giao điểm bằng 2 .

Bài II  Giải bài toán bằng cách lập phương trình hoạc hệ phương trình

Một đội xe theo kế hoạch chở hết 120 tấn hàng trong một số ngày quy định. Do mỗi ngày đội đó chở vượt mức 5 tấn nên đội đã hoàn thành kế hoạch sớm hơn thời gian quy định 1 ngày và chở thêm được 5 tấn. Hỏi theo kế hoạch đội xe chở hết số hàng đó trong bao nhiêu ngày?

Bài III. 

Cho đường tròn \(\left( O \right)\) có dây cung \(C{\rm{D}}\) cố định. Gọi M là điểm nằm chính giữa cung nhỏ \(C{\rm{D}}\).

Đường kính MN của đường tròn \(\left( O \right)\) cắt dây \(C{\rm{D}}\) tại I. Lấy điểm E bất kỳ trên cung lớn \(C{\rm{D}}\).

(E khác C,D,N); ME cắt CD tại K. Các đường thẳng NE và CD cắt nhau tại P.

a) Chứng minh rằng :Tứ giác IKEN nội tiếp

b) Chứng minh: EI.MN=NK.ME

c) NK cắt MP tại Q. Chứng minh: IK là phân giác của \(\widehat {EIQ}\)

d) Từ C vẽ đường thẳng vuông góc với EN cắt đường thẳng DE tại H. Chứng minh khi E di động trên cung lớn \(C{\rm{D}}\) (E khác C, D, N) thì H luôn chạy trên một đường cố định.

Bài IV : Cho \(a;b;c > 0\), chứng minh rằng:

\(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} < \sqrt {\dfrac{a}{{b + c}}}  \)\(\,+ \sqrt {\dfrac{b}{{c + a}}}  + \sqrt {\dfrac{c}{{a + b}}} \)

Thay \(m =  - 2\) vào phương trình ta được

Vậy đáp án B.

Câu 3. \(AC = R \Rightarrow \Delta AOC\) là tam giác đều. Suy ra góc \(CAB = {60^0}\)

Mà \(\widehat {CAB} = \dfrac{1}{2}\) số đo cung BC \( \Rightarrow \) số đo cung BC = 120⁰.

Chọn đáp án B.

Câu 4. Gọi bán kính hình tròn là R

            Chu vi hình tròn bằng \(2\pi R = 10\pi  \Rightarrow R = 5\)

Diện tích hình tròn là \(\pi {R^2} = 25\pi \left( {c{m^2}} \right)\)

Vậy chọn đáp án D.

II. TỰ LUẬN 

Bài I 

1) \(\left\{ {\begin{array}{*{20}{c}}{\dfrac{2}{{x - 2}} + \dfrac{1}{{y + 1}} = 3}\\{\dfrac{3}{{x - 2}} - \dfrac{2}{{y + 1}} = 8}\end{array}} \right.\)  ( Điều kiện xác định : \(x \ne 2;y \ne  - 1\) )

+) Đặt \(\dfrac{1}{{x - 2}} = a;\dfrac{1}{{y + 1}} = b\)

+) Hệ phương trình \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2a + b = 3}\\{3a - 2b = 8}\end{array}} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{4a + 2b = 6}\\{3a - 2b = 8}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{7a = 14}\\{3a - 2b = 8}\end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 2}\\{b =  - 1}\end{array}} \right.(TM)\end{array}\)

+) Thay \(a = 2 \Rightarrow \dfrac{1}{{x - 2}} = 2 \)

\(\Leftrightarrow 2x - 4 = 1 \Leftrightarrow x = \dfrac{5}{2}\)

+) Thay \(b =  - 1 \Rightarrow \dfrac{1}{{y + 1}} =  - 1 \) \(\Rightarrow  - y - 1 = 1 \Leftrightarrow y =  - 2\)

+) Vậy hệ phương trình có nghiệm (\(x;y) = (\dfrac{5}{2}; - 2)\)

2) Trong mặt phẳng tọa độ \({\rm{O}}xy\) cho Parabol (P) : \(y = {x^2}\) và đường thẳng (d) : \(y = 2mx - 2m + 1\)

a)

+) Phương trình hoành độ giao điểm của (P) và (d) là :

\(\begin{array}{l} \Rightarrow {x^2} = 2mx - 2m + 1\\ \Leftrightarrow {x^2} - 2mx + 2m - 1 = 0\end{array}\)

+) Thay \(m =  - 1\)  vào phương trình ta được :

\(\begin{array}{l} \Rightarrow {x^2} + 2x - 3 = 0\\ \Leftrightarrow (x - 1)(x + 3) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x =  - 3}\end{array} \Rightarrow \left[ {\begin{array}{*{20}{c}}{y = 1}\\{y = 9}\end{array}} \right.} \right.\end{array}\)

+) Vậy khi \(m =  - 1\) thì giao điểm của (P) và (d) là : \((1;1);( - 3;9)\)

b)

+) Phương trình hoành độ giao điểm của (P) và (d) là :

\(\begin{array}{l} \Rightarrow {x^2} = 2mx - 2m + 1\\ \Leftrightarrow {x^2} - 2mx + 2m - 1 = 0\end{array}\)

\(\Delta ' = {m^2} - 2m + 1 = {(m - 1)^2} > 0\) \(\forall m \ne 1\) (1)

   +) Suy ra (d) và (P) cắt nhau tại 2 điểm phân biệt  : \(A({x_1};{y_2});B({x_2};{y_2})\) 

\({x_1} \in (P) \Rightarrow {y_1} = x_1^2\)

\({x_2} \in (P) \Rightarrow {y_2} = x_2^2\)

+) Áp dụng định lí viet ta có : \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = 2m}\\{{x_1}{x_2} = 2m - 1}\end{array}} \right.\)

+) Vì tổng các tung độ của hai giao điểm bằng 2  nên ta có phương trình :

\(\begin{array}{l} \Rightarrow {y_1} + {y_2} = 2\\ \Leftrightarrow x_1^2 + x_2^2 = 2\\ \Leftrightarrow {({x_1} + {x_2})^2} - 2{x_1}{x_2} = 2\\ \Leftrightarrow 4{m^2} - 2(2m - 1) = 2\\ \Leftrightarrow 4{m^2} - 4m = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 0(TM)}\\{m = 1(Loai)}\end{array}} \right.\end{array}\)

+) Vậy \(m = 0\) thì  (d) và (P) cắt nhau tại 2 điểm phân biệt  : \(A({x_1};{y_2});B({x_2};{y_2})\) sao cho tổng các tung độ của hai giao điểm bằng 2 .

Bài II  Giải bài toán bằng cách lập phương trình hoạc hệ phương trình

Gọi thời gian chở hàng theo kế hoạch là x (ngày,\(x{\rm{ }} > {\rm{ }}1\) )

Năng suất của đội xe theo kế hoạch  là \(\dfrac{{120}}{x}\) (tấn/ngày)

Thời gian chở hàng thực tế là \(x - 1\) (ngày)

Năng suất thực tế là \(\dfrac{{125}}{{x - 1}}\) (tấn/ngày)

Vì đội xe chở hàng vượt mức 5 tấn/ ngày nên ta có phương trình

\(\begin{array}{l}\dfrac{{125}}{{x - 1}} - \dfrac{{120}}{x} = 5\\ \Rightarrow 5{x^2} - 10x - 120 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 6\\x =  - 4\end{array} \right.\end{array}\)

Vì \(x{\rm{ }} > {\rm{ }}1\)nên \(x{\rm{ }} = {\rm{ }}6\)

Vậy thời gian chở hàng theo kế hoạch là 6 ngày

Bài III. 

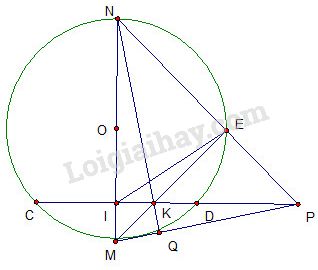
a) Xét đường tròn \(\left( O \right)\) có đường kính MN, M là điểm chính giữa cung nhỏ \(C{\rm{D}}\) (gt) nên MN vuông góc với CD tại trung điểm I của CD. Do đó: \(\widehat {MI{\rm{D}}} = {90^0}\)

Ta có \(E \in \left( {O;\dfrac{1}{2}MN} \right) \Rightarrow \widehat {MEN} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

Xét tứ giác IKEN có: \(\widehat {MI{\rm{D}}} + \widehat {MEN} = {90^0} + {90^0} = {180^0}\)mà 2 góc này ở vị trí đối nhau nên tứ giác IKEN nội tiếp. (theo dấu hiệu nhận biết tứ giác nội tiếp)

b) Tứ giác IKEN nội tiếp (cmt) nên \(\widehat {MEI} = \widehat {MNK}\) (2 góc nội tiếp cùng chắn cung \(IK\))

Xét \(\Delta MEI\) và \(\Delta MNK\)có:

\(\left. \begin{array}{l}\widehat {MEI} = \widehat {MNK}(cmt)\\\widehat {EMI}chung\end{array} \right\} \)\(\,\Rightarrow \Delta MEI \sim \Delta MNK(g.g) \)\(\,\Rightarrow \dfrac{{EI}}{{NK}} = \dfrac{{ME}}{{MN}} \)\(\,\Rightarrow EI.MN = NK.ME\)

c) Xét \(\Delta MNP\)có 2 đường cao ME và PI cắt nhau tại K nên K là trực tâm \(\Delta MNP\)

Do đó NK vuông góc với MP tại Q. Từ đó suy ra \(\widehat {NQP} = {90^0}\)

Xét tứ giác NIQP có: \(\widehat {NIP} = \widehat {NQP} = {90^0}\) mà 2 góc này cùng nhìn NP do đó tứ giác NIQP nội tiếp. Suy ra \(\widehat {QNP} = \widehat {QIP}\) (vì cùng chắn cung PQ) (1)

Tứ giác IKEN nội tiếp (cm a) nên \(\widehat {QNP} = \widehat {EIK}\)(cùng chắn cung\(EK\)) (2)

Từ (1) và (2) suy ra \(\widehat {QIP} = \widehat {EIK}\). Do đó IK là phân giác của \(\widehat {EIQ}\).

d)  Từ C vẽ đường thẳng vuông góc với EN cắt đường thẳng DE tại H. Chứng minh khi E di động trên cung lớn \(C{\rm{D}}\) (E khác C, D, N) thì H luôn chạy trên một đường cố định.

 Ta có: \(\left. \begin{array}{l}ME \bot NP\\CH \bot NP\end{array} \right\} \Rightarrow ME//CH \)\(\,\Rightarrow \left\{ \begin{array}{l}\widehat {DEM} = \widehat {DHC}\,\left( {dv} \right)\\\widehat {MEC} = \widehat {ECH}\,\left( {slt} \right)\end{array} \right.\)

Mà \(\widehat {DEM} = \widehat {MEC}\,\)( 2 góc nt chắn 2 cung = nhau)

\( \Rightarrow \widehat {EHC} = \widehat {ECH}\)

\( \Rightarrow \Delta EHC\)cân tại E

\( \Rightarrow \)EN là trung trực của CH

Xét \(\Delta DCH\)có: IN là trung trực của CD (dễ dãng cm) \( \Rightarrow NC = ND\)

                         EN là trung trực của CH (cmt)  \( \Rightarrow NC = NH\)

\( \Rightarrow \)N là tâm đường tròn ngoại tiếp \(\Delta DCH\)

\( \Rightarrow \)\(H \in \left( {N;NC} \right)\)

Mà N, C cố định => H thuộc đường tròn cố định khi E chạy trên CD

Bài IV 

Đặt \(A = \dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}} \)\(\,= 1 - \dfrac{b}{{a + b}} + 1 - \dfrac{c}{{b + c}} + 1 \)\(\,- \dfrac{a}{{c + a}}\)\(\, = 3 - \left( {\dfrac{b}{{a + b}} + \dfrac{c}{{b + c}} + \dfrac{a}{{c + a}}} \right)\)

Mà do \(a;b;c > 0\)nên:

\(\dfrac{b}{{a + b}} > \dfrac{b}{{a + b + c}}\)

\(\dfrac{c}{{b + c}} > \dfrac{c}{{a + b + c}}\)

\(\dfrac{a}{{c + a}} > \dfrac{a}{{a + b + c}}\)

Cộng các vế ta được:

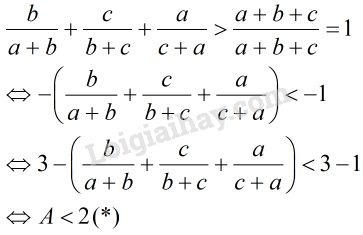
Đặt \(B = \sqrt {\dfrac{a}{{b + c}}}  + \sqrt {\dfrac{b}{{c + a}}}  + \sqrt {\dfrac{c}{{a + b}}} \)\(\,= \dfrac{a}{{\sqrt {a(b + c)} }} \)\(\,+ \dfrac{b}{{\sqrt {b(c + a)} }} + \dfrac{c}{{\sqrt {c(a + b)} }}\)

Áp dụng bất đẳng thức Cô si cho 2 số dương \(\sqrt a ;\sqrt {b + c} \)ta được:

\(\sqrt {a(b + c)}  \le \dfrac{{a + b + c}}{2} \)

\(\Leftrightarrow \dfrac{a}{{\sqrt {a(b + c)} }} \ge \dfrac{{2a}}{{a + b + c}}\)

Tương tự ta có:

\(\dfrac{b}{{\sqrt {b(c + a)} }} \ge \dfrac{{2b}}{{a + b + c}}\)

\(\dfrac{c}{{\sqrt {c(a + b)} }} \ge \dfrac{{2c}}{{a + b + c}}\)

Từ đó, ta có:

\(\dfrac{a}{{\sqrt {a(b + c)} }} + \dfrac{b}{{\sqrt {b(c + a)} }} \)\(\,+ \dfrac{c}{{\sqrt {c(a + b)} }} \ge \dfrac{{2a + 2b + 2c}}{{a + b + c}} = 2\)

\( \Leftrightarrow B \ge 2\,\,(**)\)

Từ \((*),(**)\)ta có: \(A < B\) hay \(\dfrac{a}{{a + b}} + \dfrac{b}{{b + c}} + \dfrac{c}{{c + a}}\)\(\, < \sqrt {\dfrac{a}{{b + c}}}  + \sqrt {\dfrac{b}{{c + a}}}  + \sqrt {\dfrac{c}{{a + b}}} \)

=> đpcm

Bài 1.  Cho hai biểu thức \(A = \dfrac{{x + 12}}{{\sqrt x  - 1}}\) và \(B = \left( {\dfrac{3}{{x - 1}} + \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{1}{{\sqrt x  + 1}}\) với \(x \ge 0,x \ne 1\)

a) Tính giá trị của biểu thức A khi x = 9

b) Rút gọn biểu thức B

c) Tìm giá trị nhỏ nhất của biểu thức \(M = \dfrac{A}{B}\)

Bài 2.  Giải bài toán bằng cách lập phương trình

Một công nhân dự định làm 33 sản phẩm trong thời gian đã định. Nhưng thực tế xí nghiệp lại giao 62 sản phẩm. Do vậy mặc dù người đó đã làm tăng mỗi giờ 3 sản phẩm song vẫn hoàn thành chậm hơn dự định 1 giờ 30 phút. Tính năng suất dự định.

Bài 3. 

1) Giải hệ phương trình: \(\left\{ \begin{array}{l}3\sqrt {x - 3}  - \dfrac{1}{{y + 1}} = 1\\\sqrt {x - 3}  + \dfrac{2}{{y + 1}} = 5\end{array} \right.\)

2) Cho Parabol \(y = {x^2}\) (P) và đường thẳng \(y = mx - m + 1\) (d).

  a) Tìm tọa độ giao điểm của (P) và (d) với m = - 3.

  b) Tìm m để đường thẳng (d) và parabol (P) cắt nhau tại hai điểm phân biệt có hoành độ \({x_1},{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = {x_1} + {x_2}\).

Bài 4. Cho đường tròn (O; R), đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn (O; R) sao cho đoạn thẳng AC cắt đường tròn (O; R) tại điểm K khác A, hai dây MN và BK cắt nhau ở E.

a) Chứng minh rằng AHEK là tứ giác nội tiếp.

b) Chứng minh CA . CK = CE . CH

c) Qua N kẻ đường thẳng vuông góc với AC cắt tia MK tại F. Chứng minh \(\Delta NFK\)cân.

d) Giả sử KE = KC. Chứng minh OK // MN

Bài 5.  Cho a, b, c là độ dài 3 cạnh của một tam giác biết:

a + b – c > 0; b + c – a > 0;  c + a – b > 0

Chứng minh: \(\dfrac{1}{{a + b - c}} + \dfrac{1}{{b + c - a}} + \dfrac{1}{{c + a - b}} \)\(\,\ge \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}\)

\( \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - \left( {{x_1} + {x_2}} \right) = 0\)

\( \Leftrightarrow {m^2} - 2(m - 1) - m = 0\)

\( \Leftrightarrow {m^2} - 3m + 2 = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}m = 1(TM)\\m = 2(L)\end{array} \right.\)

Bài 4:

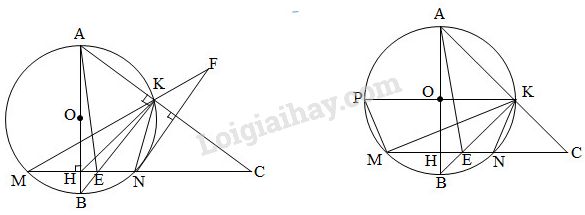
a) Ta có: \(\widehat {AHE} = {90^0}\) (theo giả thiết \(AB \bot MN)\)

\(\widehat {AKE} = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

\( \Rightarrow \widehat {AHE} + \widehat {AKE} = {180^0}\). Vậy tứ giác AHEK là tứ giác nội tiếp. (Tổng hai góc đối bằng 180⁰)

b) Xét hai tam giác CAE và CHK:

+ Có góc C chung

+ \(\widehat {EAC} = \widehat {EHK}\) (góc nội tiếp cùng chắn cùng EK)

Suy ra ∆CAE ~ ∆CHA (g – g)

Suy ra CA . CK = CE . CH

Hoặc cm ∆CKE ~ ∆CHA (g –g )

c) Do đường kính AB vuông góc MN nên B là điểm chính giữa cung MN

Suy ra \(\widehat {MKB} = \widehat {NKB}\) (1)

Lại có BK // NF (vì cùng vuông góc với AC) nên \(\left\{ \begin{array}{l}\widehat {NKB} = \widehat {KNF}(2)\\\widehat {MKB} = \widehat {MFN}(3)\end{array} \right.\)

Từ (1), (2), (3) suy ra \(\widehat {MFN} = \widehat {KNF} \Leftrightarrow \widehat {KFN} = \widehat {KNF}\). Vậy \(\Delta KNF\) cân tại K.

d) Ta có \(\widehat {AKB} = {90^0} \Rightarrow \widehat {BKC} = {90^0} \)

\(\Rightarrow \Delta KEC\) vuông tại K.

Theo giả thiết ta lại có KE = KC nên tam giác KEC vuông cân tại K

\(\widehat {BEH} = \widehat {KEC} = {45^0} \Rightarrow \widehat {OBK} = {45^0}\)

Mặt khác vì tam giác OBK cân tại O (do OB = OK = R) nên suy ra tam giác OBK vuông cân tại O dẫn đến OK // MN (cùng vuông góc với AB)

Bài 5. 

Áp dụng bất đẳng thức Côsi

Với x > 0, y > 0 ta có \(x + y \ge 2\sqrt {xy} \)

\({(x + y)^2} \ge 4xy \Leftrightarrow \dfrac{{x + y}}{{xy}} \ge \dfrac{4}{{x + y}}\)

\(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}(*)\)

Dấu “=” xảy ra \( \Leftrightarrow x = y\)

Áp dụng BĐT (*) ta có:

\(\dfrac{1}{{a + b - c}} + \dfrac{1}{{b + c - a}} \)\(\,\ge \dfrac{4}{{a + b - c + b + c - a}} = \dfrac{4}{{2b}} \)\(\,= \dfrac{2}{b}(1)\)

Tương tự: \(\dfrac{1}{{c + a - b}} + \dfrac{1}{{b + c - a}} \ge \dfrac{2}{c}(2)\)

                  \(\dfrac{1}{{c + a - b}} + \dfrac{1}{{a + b - c}} \ge \dfrac{2}{a}(3)\)

Cộng (1), (2), (3) vế với vế ta có:

\(\dfrac{1}{{a + b - c}} + \dfrac{1}{{b + c - a}} + \dfrac{1}{{c + a - b}}\)\(\, \ge \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}\) . Dấu “=” xảy ra \( \Leftrightarrow a = b = c\)