Diễn biến tâm trạng của Mị trong " đêm tình mùa xuân" (Vợ chồng A Phủ)
Lời giải
Bài Tập và lời giải
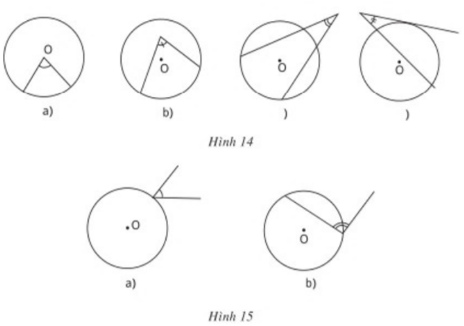
Vì sao các góc ở hình 14 và hình 15 không phải là góc nội tiếp ?
Các khẳng định sau đúng hay sai?
a) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
b) Trong một đường tròn, các góc nội tiếp bằng nhau thì cùng chắn một cung.
Xem hình 19 ( hai đường tròn có tâm là B, C và điểm B nằm trên đường tròn tâm C).
a) Biết \(\widehat{MAN}\) = \(30^{\circ}\), tính \(\widehat{PCQ}\).
b) Nếu \(\widehat{PCQ}\) =\(136^{\circ}\) thì \(\widehat{MAN}\) có số đo là bao nhiêu?

Muốn xác định tâm của một đường tròn mà chỉ dùng êke thì phải làm như thế nào?
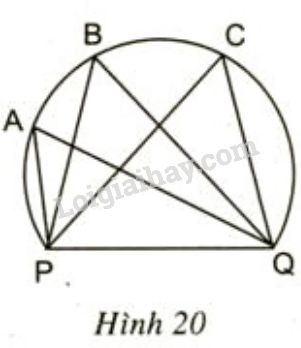
Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn \(PQ\). Bóng được đặt ở các vị trí \(A, B, C\) trên một cung tròn như hình 20.
Hãy so sánh các góc \(\widehat{PAQ}\), \(\widehat{PBQ}\), \(\widehat{PCQ}\).
Cho một đường tròn tâm \(O\), đường kính \(AB\) và \(S\) là một điểm nằm ngoài đường tròn. \(SA\) và \(SB\) lần lượt cắt đường tròn tại \(M, N\). Gọi \(H\) là giao điểm của \(BM\) và \(AN\). Chứng minh rằng \(SH\) vuông góc với \(AB\).
Cho hai đường tròn \((O)\) và \((O')\) cắt nhau tại \(A\) và \(B\). Vẽ các đường kính \(AC\) và \(AD\) của hai đường tròn. Chứng minh rằng ba điểm \(C, B, D\) thẳng hàng.
Cho hai đường tròn bằng nhau \((O)\) và \((O')\) cắt nhau tại \(A\) và \(B\). Vẽ đường thẳng qua \(A\) cắt \(O\) tại \(M\) và cắt \((O')\) tại \(N\) ( \(A\) nằm giữa \(M\) và \(N\)). Hỏi \(MBN\) là tam giác gi? Tại sao?
Trên đường tròn \((O)\) đường kính \(AB\), lấy điểm \(M\) (khác \(A\) và \(B\)). Vẽ tiếp tuyến của (O) tại \(A\). Đường thẳng \(BM\) cắt tiếp tuyến đó tại \(C\). Chứng minh rằng ta luôn có: \(M{A^2} = MB.MC\)
Cho đường tròn \((O)\) và một điểm \(M\) cố định không nằm trên đường tròn. Qua \(M\) kẻ hai đường thẳng. Đường thẳng thứ nhất cắt \((O)\) tại \(A\) và \(B\).Đường thẳng thứ nhất cắt \((O)\) tại \(C\) và \(D\).
Chứng minh \(MA. MB = MC. MD\)
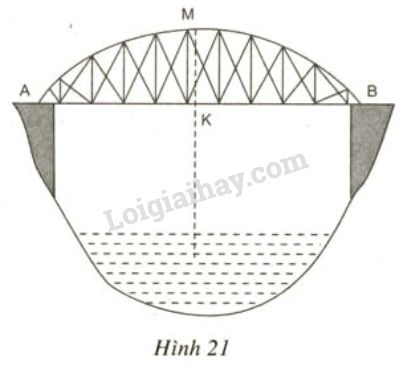
Một chiếc cầu được thiết kế như hình 21 có độ dài \(AB = 40\)m, chiều cao \(MK = 3\)m. Hãy tính bán kính của đường tròn chứa cung \(AMB\)
Dựng một tam giác vuông, biết cạnh huyền dài \(4\)cm và một cạnh góc vuông dài \(2,5\) cm.
Cho \(AB, BC, CA \) là ba dây của đường tròn \((O)\). Từ điểm chính giữa \(M\) của \(\overparen{AB}\) vẽ dây \(MN\) song song với dây \(BC\). Gọi giao điểm của \(MN\) và \(AC\) là \(S\). Chứng minh \(SM = SC\) và \(SN = SA\)
Cho ∆ABC ( AB < AC) nội tiếp trong đường tròn (O). Lấy D trên cạnh BC, AD cắt cung BC ở E. Chứng minh rằng :
a)\(\widehat {AEC} > \widehat {AEB}\)
b) \(AB. CD = AD . CE\)
Cho ∆ABC nội tiếp đường tròn (O). Tia phân giác của góc A cắt BC ở D và cắt đường tròn ở E. Chứng minh rằng:
a) \(AB . AC = AD . AE\)
b) \(B{E^2} = AE.DE.\)
Từ một điểm P nằm ngoài đường tròn (O; R), kẻ hai tiếp tuyến PA, PB đến (O) ( A, B là hai tiếp điểm). Trên dây AB lấy M bất kì. Qua M kẻ đường vuông góc với OM cắt PA tại S và PB tại Q. Chứng minh rằng: \(MS = MQ\).
