Phân tích diễn biến tâm lí của nhân vật Mị trong đêm tình mùa xuân
Lời giải
Bài Tập và lời giải
Chu vi hình chữ nhật \(ABCD\) là \(20cm\). Hãy tìm giá trị nhỏ nhất của độ dài đường chéo \(AC\).
Tam giác \(ABC\) có góc \(\widehat B = {45^0},\) góc \(\widehat C = {30^0}.\) Nếu \(AC = 8\) thì \(AB\) bằng:
(A) \(4\) (B) \(4\sqrt2\)
(C) \(4\sqrt3\) (D) \(4\sqrt6\)
Hãy chọn câu trả lời đúng.
Cho tam giác \(ABC\) vuông ở \(C\) có đường trung tuyến \(BN\) vuông góc với đường trung tuyến \(CM,\) cạnh \(BC = a.\) Tính độ dài đường trung tuyến \(BN.\)
Nếu tam giác vuông \(ABC\) vuông tại \(C\) và có \(\displaystyle \sin {\rm{A}} = {2 \over 3}\) thì \(tan B\) bằng:
(A) \(\displaystyle {3 \over 5}\) (B) \(\displaystyle {{\sqrt 5 } \over 3}\) (C) \(\displaystyle{2 \over {\sqrt 5 }}\) (D) \(\displaystyle {{\sqrt 5 } \over 2}\)
Hãy chọn câu trả lời đúng.
Tam giác \(ABC\) vuông tại \(C\) có \(AC = 15cm.\) Đường cao \(CH\) chia \(AB\) thành hai đoạn \(AH\) và \(HB.\) Biết \(HB = 16cm.\) Tính diện tích tam giác \(ABC.\)
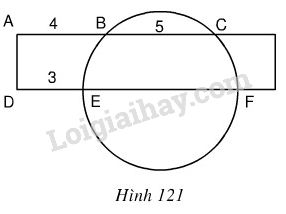
Một hình chữ nhật cắt đường tròn như hình 121 biết \(AB = 4, BC = 5, DE = 3\) (với cùng đơn vị đo).
Độ dài \(EF\) bằng:
(A) \(6\) (B) \(7\) (C) \(\displaystyle {{20} \over 3}\) (D) \(8\)
Hãy chọn câu trả lời đúng.
Cho tam giác đều \(ABC\), \(O\) là trung điểm của \(BC\). Trên các cạnh \(AB, AC\) lần lượt lấy các điểm di động \(D\) và \(E\) sao cho góc \(\widehat {DOE} = {60^0}\).
a) Chứng minh tích \(BD.CE\) không đổi.
b) Chứng minh \(ΔBOD\) đồng dạng \(ΔOED\). Từ đó suy ra tia \(DO\) là tia phân giác của góc \(BDE\).
c) Vẽ đường tròn tâm \(O\) tiếp xúc với \(AB\). Chứng minh rằng đường tròn này luôn tiếp xúc với \(DE\).
Cho hai đường tròn \((O; R)\) và \((O'; r)\) tiếp xúc ngoài \((R > r).\) Hai tiếp tuyến chung \(AB\) và \(A'B'\) của hai đường tròn \((O)\) và \((O')\) cắt nhau tại \(P\) (\(A\) và \(A'\) thuộc đường tròn \((O'),\) \(B\) và \(B'\) thuộc đường tròn \((O)\)). Biết \(PA = AB = 4 cm.\) Tính diện tích hình tròn \((O').\)
Cho tam giác \(ABC\) nội tiếp đường tròn \((O'\)) và ngoại tiếp đường tròn \((O)\). Tia \(AO\) cắt đường tròn \((O')\) tại \(D\). Ta có:
(A) \(CD = BD = O'D\) ; (B) \(AO = CO = OD\)
(C) \(CD = CO = BD\) ; (D) \(CD = OD = BD\)
Hãy chọn câu trả lời đúng.
Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \((O)\). Các cung nhỏ \(AB, BC, CA\) có số đo lần lượt là \(x + 75^0, 2x + 25^0, 3x - 22^0\). Một góc của tam giác \(ABC\) có số đo là:
(A) \(57^05\) ; (B) \(59^0\) ; (C) \(61^0\) ; (D) \(60^0\)
Hãy chọn câu trả lời đúng.
Từ một điểm \(P\) ở ngoài đường tròn \((O)\), kẻ cát tuyến \(PAB\) và \(PCD\) tới đường tròn. Gọi \(Q\) là một điểm nằm trên cung nhỏ \(BD\) (không chứa \(A\) và \(C\)) sao cho \(sđ\overparen{BQ}=42^0\) và \(sđ\overparen{QD}=38^0\). Tính tổng \(\widehat {BP{\rm{D}}} + \widehat {AQC}.\)
Một hình vuông và một hình tròn có chu vi bằng nhau. Hỏi hình nào có diện tích lớn hơn?
Ta lập tỉ số diện tích hình vuông và hình tròn:
\(\displaystyle {{{S_{hv}}} \over {{S_{htr}}}} = {{{a^2}} \over {\pi {R^2}}}\) \(=\displaystyle {{{{\left( {{{\pi R} \over 2}} \right)}^2}} \over {\pi {R^2}}}\) \(\displaystyle ={{{\pi ^2}{R^2}} \over {4\pi {R^2}}} = {\pi \over 4} < 1\) (vì \(π ≈ 3,14\))
\(\Rightarrow {S_{hv}} < {S_{htr}}\)
Vậy hình tròn có diện tích lớn hơn hình vuông.
Cho đường tròn \((O)\), cung \(BC\) có số đo bằng \(120^0\), điểm \(A\) di chuyển trên cung lớn \(BC\). Trên tia đối tia \(AB\) lấy điểm \(D\) sao cho \(AD = AC\). Hỏi điểm \(D\) di chuyển trên đường nào?
Dựng tam giác \(ABC\), biết \(BC = 4cm\), góc \(\widehat {A} = 60^0\), bán kính đường tròn nội tiếp tam giác bằng \(1cm\).
Tam giác \(ABC\) cân tại \(A\) có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn \((O).\) Tiếp tuyến tại \(B\) và \(C\) của đường tròn lần lượt cắt tia \(AC\) và tia \(AB\) ở \(D\) và \(E.\) Chứng minh:
a) \(BD^2 = AD.CD.\)
b) Tứ giác \(BCDE\) là tứ giác nội tiếp.
c) \(BC\) song song với \(DE.\)
Một mặt phẳng chứa trụ \(OO'\) của một hình trụ; phần mặt phẳng nằm trong hình trụ là một hình chữ nhật có chiều dài \(3cm\), chiều rộng \(2cm.\) Tính diện tích xung quanh và thể tích hình trụ đó.
Khi quay tam giác \(ABC\) vuông ở \(A\) một vòng quanh cạnh góc vuông \(AC\) cố định, ta được một hình nón. Biết rằng \(BC = 4dm,\) góc \(\widehat {ACB} = {30^0}.\) Tính diện tích xung quanh và thể tích hình nón.
Một hình cầu có số đo diện tích (đơn vị: \(m^2\)) bằng số đo thể tích (đơn vị: \(m^3\)). Tính bán kính hình cầu, diện tích mặt cầu và thể tích hình cầu.
Ta có: \(S = 4πR^2 = 4π . 3^2= 36π\) (\(m^2\))
\(\displaystyle V = {4 \over 3}\pi {R^3} = {4 \over 3}\pi {.3^3} = 36\pi \left( {{m^3}} \right)\).
