Giá trị nhân văn của truyện ngắn Vợ chồng A Phủ

Bài 1 (1,5 điểm)

1) Rút gọn biểu thức \(A = {\left( {\sqrt 5  - \sqrt 2 } \right)^2} + \sqrt {40} \)

2) Rút gọn biểu thức \(B = \left( {\dfrac{{x - \sqrt x }}{{\sqrt x  - 1}} - \dfrac{{\sqrt x  + 1}}{{x + \sqrt x }}} \right):\dfrac{{\sqrt x  + 1}}{{\sqrt x }}\) với \(x > 0,\,\,x \ne 1\)

Tính giá trị của B khi \(x = 12 + 8\sqrt 2 \)

Bài 2 (1,5 điểm)

Cho Parabol \(\left( P \right):\;\;y =  - {x^2}\) và đường thẳng \(\left( d \right):\;\;y = 2\sqrt 3 x + m + 1\) (m là tham số).

1) Vẽ đồ thị hàm số (P).

2) Tìm tất cả các giá trị của tham số m để (d) cắt (P) tại hai điểm phân biệt.

Bài 3 (2,0 điểm)

1) Giải hệ phương trình: \(\left\{ \begin{array}{l}9x + y = 11\\5x + 2y = 9\end{array} \right.\)

2) Cho phương trình: \({x^2} - 2\left( {m + 2} \right)x + {m^2} + 3m - 2 = 0\,\,\left( 1 \right)\), (m là tham số)

a. Giải phương trình (1) khi m = 3.

b. Tìm các giá trị của tham số m để phương trình (1)  có hai nghiệm phân biệt \({x_1},{x_2}\) sao cho biểu thức \(A = 2018 + 3{x_1}{x_2} - x_1^2 - x_2^2\) đạt giá trị nhỏ nhất.

Bài 4  (1,5 điểm)

Một người dự định đi xe máy từ tỉnh A đến tỉnh B cách nhau 90 km trong một thời gian đã định. Sau khi đi được 1 giờ, người đó nghỉ 9 phút. Do đó, để đến tỉnh B đúng hẹn, người ấy phải tăng vận tốc thêm 4 km/h. Tính vận tốc lúc đấy của người đó.

Bài 5  (3,5 điểm)

Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn (O) có bán kính \(R = 3cm\). Các tiếp tuyến với (O) tại B và C cắt nhau tại D.

1) Chứng minh tứ giác OBDC nội tiếp đường tròn.

2) Gọi M là giao điểm của BC và OD. Biết \(OD = 5cm\). Tính diện tích của tam giác BCD.

3) Kẻ đường thẳng d đi qua D và song song với đường tiếp tuyến với (O) tại A, d cắt các đường thẳng AB, AC lần lượt tại P, Q. Chứng minh \(AB.AP = AQ.AC\)

4) Chứng minh góc PAD bằng góc MAC.

Bài 1. 

1. Rút gọn biểu thức \(2\sqrt {75}  + 3\sqrt {48}  - 4\sqrt {27} \)

2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 8\\3x + 2y = 5\end{array} \right.\)

3. Giải phương trình \(3{x^2} - 7x + 2 = 0\)

Bài 2. 

Cho hai hàm số: \(y =  - x + 2\) và \(y = {x^2}\) có đồ thị lần lượt là \(\left( d \right)\)  và \(\left( P \right).\)

1) Vẽ  \(\left( d \right)\)  và \(\left( P \right)\) trên cùng hệ trục tọa độ.

2)  Bằng phép toán tìm tọa độ giao điểm của  \(\left( d \right)\)  và \(\left( P \right).\)

Bài 3. Cho phương trình \({x^2} - \left( {m + 1} \right)x + m - 2 = 0\) (với m là tham số).

1) Chứng minh phương trình luôn có hai nghiệm phân biệt với mọi m.

2) Tìm các số nguyên m để phương trình có nghiệm nguyên.

Bài 4. Cho tam giác ABC vuông tại A, đường cao AH \(\left( {H \in BC} \right)\) . Biết BH = 3,6cm và HC = 6,4 cm. Tính độ dài BC, AH, AB, AC.

Bài 5. 

 Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), M là trung điểm của cạnh AC. Đường tròn đường kính  MC cắt BC tại N. Đường thẳng BM cắt đường tròn đường kính MC tại D.

1. Chứng minh tứ giác BADC nội tiếp.

2. Chứng minh DB là phân giác của góc ADN.

3. BA và CD kéo dài cắt nhau tại P. Chứng minh ba điểm P, M, N thẳng hàng.

Câu 1.

1. Tính giá trị của các biểu thức

\(M = \sqrt {36}  + \sqrt {25} \)                               

\(N = \sqrt {{{\left( {\sqrt 5  - 1} \right)}^2}}  - \sqrt 5 \)

2. Cho biểu thức \(P = 1 + \dfrac{{x - \sqrt x }}{{\sqrt x  - 1}},\) với \(x \ge 0\) và \(x \ne 1\)

a) Rút gọn biểu thức P

b) Tìm giá trị của x, biết P > 3

Câu 2.

1) Cho parabol \(\left( P \right):\;y = {x^2}\)  và  đường thẳng \(\left( d \right):\;y =  - x + 2.\)

a) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng một mặt phẳng tọa độ Oxy.

b)  Tìm tọa độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) bằng phép tính.

2) Không sử dụng máy tính, giải hệ phương trình sau: \(\left\{ \begin{array}{l}3x + y = 5\\2x - y = 10\end{array} \right..\)

Câu 3. 1) Cho phương trình \({x^2} - 2mx + 2m - 1 = 0\) (m là tham số)   (1)   

a)  Giải phương trình (1) với \(m = 2.\)

b) Tìm \(m\) để phương trình (1) có hai nghiệm \({x_1},\;{x_2}\) sao cho: \(\left( {x_1^2 - 2m{x_1} + 3} \right)\left( {x_2^2 - 2m{x_2} - 2} \right) = 50.\)

2) Quãng đường AB dài 50 km. Hai xe máy khởi hành cùng một lúc từ A đến B. Vận tốc xe thứ nhất lớn hơn vận tốc xe thứ hai 10 km/h, nên xe thứ nhất đến B trước xe thứ hai 15 phút. Tính vận tốc của mỗi xe.

Câu 4. Cho tam giác ABC vuông tại A, đường cao AH \(\left( {H \in BC} \right)\) . Biết AC = 8cm và BC = 10 cm. Tính độ dài AB, BH, CH  và AH.

Câu 5. Cho đường tròn tâm (O), từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB (A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D; O và B nằm về hai phía so với cát tuyến MCD).

a) Chứng minh tứ giác MAOB nội tiếp.

b) Chứng minh \(M{B^2} = MC.MD\)

c) Gọi H là giao điểm của AB và OM. Chứng minh AB là phân giác của \(\widehat {CHD}\).

Câu 1.  Tính giá trị biểu thức \(T = \sqrt {16}  + 5\)

Câu 2. Giải phương trình \(2x - 3 = 1\)

Câu 3.  Tìm giá trị của m để đường thẳng \(\left( d \right):y = 3x + m - 2\) đi qua điểm \(A\left( {0;1} \right)\).

Câu 4. Vẽ đồ thị hàm số \(y =  - 2{x^2}\)

Câu 5. Giải hệ phương trình \(\left\{ \begin{array}{l}3x - 2y = 4\\x + 3y = 5\end{array} \right..\)

Câu 6. Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\;\left( {H \in BC} \right).\)Biết \(AB = 3a,\;\;AH = \dfrac{{12}}{5}a.\) Tính theo \(a\) độ dài \(AC\) và \(BC.\) 

Câu 7. Tìm giá trị của m để phương trình \(2{x^2} - 5x + 2m - 1 = 0\) có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) thỏa mãn: \(\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} = \dfrac{5}{2}.\)

Câu 8. Một đội máy xúc được thuê đào \(20000\;{m^3}\) đất để mở rộng hồ Dầu Tiếng. Ban đầu đội dự định mỗi ngày đào một lượng đất nhất định để hoàn thành công việc, nhưng sau khi đào được \(5000\;{m^3}\) thì đội được tăng cường thêm một số máy xúc nên mỗi ngày đào thêm được \(100\;{m^3},\) do đó đã hoàn thành công việc trong \(35\) ngày. Hỏi ban đầu đội dự định mỗi ngày đào bao nhiêu \({m^3}\) đất?

Câu 9 Cho tam giác ABC có ba góc nhọn \(\left( {AB < AC} \right)\) và có đường cao AH (H thuộc cạnh BC). Gọi D, E lần lượt là trung điểm của AB và AC. Chứng minh DE là tiếp tuyến chung của hai đường tròn lần lượt ngoại tiếp tam giác DBH và ECH.

Câu 10 :Cho đường tròn tâm O bán kính 2R (kí hiệu (O; 2R)) và đường tròn tâm O’ bán kính R (kí hiệu (O’; R)) tiếp xúc ngoài nhau tại A. Lấy điểm B trên đường tròn (O; 2R) sao cho \(\widehat {BAO} = {30^0}\), tia BA cắt đường tròn (O’; R) tại điểm C (C khác điểm A). Tiếp tuyến của đường tròn (O’; R) tại điểm C cắt đường thẳng BO tại điểm E. Tính theo R diện tích tam giác ABE.

Câu 1. 

1. Thực hiện phép tính \(\dfrac{{\sqrt {27} }}{{\sqrt 3 }}\)

2. Rút gọn biểu thức \(P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{9 + x}}{{9 - x}}} \right).\left( {3\sqrt x  - x} \right)\)  với \(x \ge 0\)  và \(x \ne 9\)

3. Xác định các hệ số a, b để đồ thị hàm số \(y = ax + b\)  đi qua hai điểm  \(A\left( {2; - 2} \right)\) và \(B\left( { - 3;2} \right)\)

Câu 2. 

1. Giải phương trình \({x^2} - 4x + 4 = 0\)

2. Tìm giá trị của m để phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3 = 0\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 10.\)

Câu 3. Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:

Một xe ô tô đi từ A đến B theo đường quốc lộ cũ dài 156 km với vận tốc không đổi. Khi từ B về A, xe đi đường cao tốc mới nên quãng đường giảm được 36 km so với lúc đi và vận tốc tăng so với lúc đi là 32 km/h. Tính vận tốc ô tô khi đi từ A đến B, biết thời gian đi nhiều hơn thời gian về là 1 giờ 45 phút.

Câu 4. 

Cho đường tròn tâm O, đường kính AB = 2R. Trên đường tròn (O) lấy điểm C bất kì (C không trùng với A và B). Tiếp tuyến của đường tròn (O) tại A cắt tia BC ở điểm D. Gọi H là hình chiếu của A trên đường thẳng DO. Tia AH cắt đường tròn (O) tại điểm F (không trùng với A). Chứng minh

a) \(D{A^2} = DC.DB\)

b) Tứ giác AHCD nội tiếp.

c) \(CH \bot CF\)

d) \(\dfrac{{BH.BC}}{{BF}} = 2R\)

Câu 5 

Cho x, y là các số thực dương thỏa mãn \(xy + 1 \le x\). Tìm giá trị nhỏ nhất của biểu thức \(Q = \dfrac{{x + y}}{{\sqrt {3{x^2} - xy + {y^2}} }}\)

Câu 1. 

a)  Rút gọn các biểu thức

\(A = \sqrt {12}  + \sqrt {27}  - \sqrt {48} \)

\(B = \left( {\dfrac{1}{{\sqrt x  - 1}} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{x + 1}}{{x - 1}}\)  với \(x \ge 0\)  và \(x \ne  \pm 1\)

b)  Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 12\\3x - y = 1\end{array} \right.\)

Câu 2. Cho phương trình \({x^2} + 5x + m = 0\left( * \right)\) (m là tham số )

a)  Giải phương trình (*) khi \(m =  - 3\)

b)  Tìm m để phương trình (*) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(9{x_1} + 2{x_2} = 18\)

Câu 3. 

Trong mặt phẳng tọa độ \(\left( {Oxy} \right),\) cho parabol \(\left( P \right):\;\;y = \dfrac{1}{2}{x^2}\) và đường thẳng \(\left( d \right):\;y = \left( {2m - 1} \right)x + 5.\)

a) Vẽ đồ thị của (P).

b) Tìm m để đường thẳng (d) đi qua điểm \(E\left( {7;\;12} \right).\)

c) Đường thẳng \(y = 2\) cắt parabol \(\left( P \right)\) tại hai điểm \(A,\;B.\) Tìm tọa độ của \(A,\;B\) và tính diện tích tam giác \(OAB.\)

Câu 4. Cho đường tròn tâm \(\left( {O;R} \right)\) có đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn \(\left( {O;R} \right)\) sao cho đoạn thẳng AC cắt đường tròn \(\left( {O;R} \right)\) tại điểm K (K khác A), hai dây MN và BK cắt nhau ở E.

a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.

b) Chứng minh CA.CK = CE.CH

c) Qua điểm N kẻ đường thẳng (d) vuông góc với AC, (d) cắt MK tại F. Chứng minh tam giác NFK cân.

d) Khi KE = KC. Chứng minh OK // MN.

Bài 1 (1,5 điểm) Cho parabol \(\left( P \right):\;\;y = {x^2}\) và đường thẳng \(\left( d \right):\;\;y = 3x - 2.\)

a) Vẽ \(\left( P \right)\)  và \(\left( d \right)\) trên cùng hệ trục tọa độ.

b) Tìm tọa độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) bằng phép tính.

Bài 2 (1 điểm). Cho phương trình \(3{x^2} - x - 1 = 0\)  có \(2\) nghiệm là \({x_1},{x_2}\). Không giải phương trình, hãy tính giá trị của biểu thức \(A = x_1^2 + x_2^2\).

Bài 3 (1 điểm). Mối quan hệ giữa thang nhiệt độ F (Fahrenheit) và thang nhiệt độ C (Celsius) được cho bởi công thức \({T_F} = 1,8.{T_C} + 32,\) trong đó \({T_C}\) là nhiệt độ tính theo độ C và \({T_F}\) là nhiệt độ tính theo độ F. Ví dụ \({T_C} = {0^0}\) C tương ứng với \({T_F} = {32^0}\) F.

a) Hỏi \({25^0}\) C tương ứng với bao nhiêu độ F ?

b) Các nhà khoa học đã tìm ra mối liên hệ giữa \(A\) là số tiếng kêu của một con dế trong một phút và \({T_F}\) là nhiệt độ cơ thể của nó bởi công thức \(A = 5,6.{T_F} - 275,\) trong đó \({T_F}\) là nhiệt độ tín theo độ F. Hỏi nếu con dế kêu 106 tiếng trong một phút thì nhiệt độ của nó khoảng bao nhiêu độ C? (làm tròn đến hàng đơn vị)

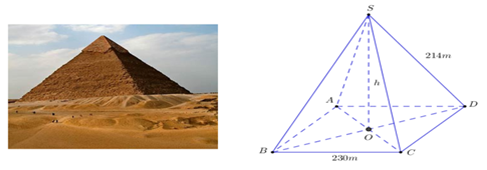
Bài 4: (0,75 điểm)Kim tự tháp Kheops – Ai Cập có dạng hình chóp đều, đáy là hình vuông, các mặt bên là các tam giác cân chung đỉnh (hình vẽ). Mỗi cạnh bên của kim tự tháp dài 214 m, cạnh đáy của nó dài 230 m.

a) Tính theo mét chiều cao h của kim tự tháp (làm tròn đến chữ số thập phân thứ nhất).

b) Cho biết thể tích của hình chóp được tính theo công thức \(V = \dfrac{1}{3}Sh\), trong đó \(S\) là diện tích mặt đáy, h là chiều cao của hình chóp. Tính theo \({m^3}\) thể tích của kim tự tháp (làm tròn đến hàng nghìn).

Bài 5 (1 điểm). Siêu thị A thực hiện chương trình giảm giá cho khách hàng mua loại túi bột giặt 4 kg như sau: Nếu mua 1 túi thì được giảm giá 10 000 đồng so với giá niêm yết. Nếu mua 2 túi thì túi thứ nhất được giảm 10 000 đồng và túi thứ hai được giảm 20 000 đồng so với giá niêm yết. Nếu mua từ 3 túi trở lên thì ngoài 2 túi đầu được hưởng chương trình giảm giá như trên, từ túi thứ ba trở đi mỗi túi sẽ được giảm 20% so với giá niêm yết.

a) Bà Tư mua 5 túi bột giặt loại 4 kg ở siêu thị A thì phải trả số tiền là bao nhiêu, biết rằng loại túi bột giặt mà bà Tư mua có giá niêm yết là 150 000 đồng/túi.

b) Siêu thị B lại có hình thức giảm giá khác cho loại túi bột giặt nêu trên là: nếu mua từ 3 túi trở lên thì sẽ giảm giá 15% cho mỗi túi. Nếu bà Tư mua 5 túi bột giặt thì bà Tư nên mua ở siêu thị nào để số tiền phải trả ít hơn? Biết rằng giá niêm yết của hai siêu thị là như nhau.

Bài 6 (1 điểm). Nhiệt độ sôi của nước không phải lúc nào cũng là \({100^0}C\) mà phụ thuộc vào độ cao của nơi đó so với mực nước biển. Chẳng hạn Thành phố Hồ Chí Minh có độ cao xem như ngang mực nước biển \(\left( {x = 0\,m} \right)\) thì nước có nhiệt độ sôi là \(y = {100^0}C\) nhưng ở thủ đô La Paz của Bolivia, Nam Mỹ có độ cao \(x = 3\,600\,m\) so với mực nước biển thì nhiệt độ sôi của nước là \(y = {87^0}C\). Ở độ cao trong khoảng vài \(km\), người ta thấy mối liên hệ giữa hai đại lượng này là một hàm số bậc nhất \(y = ax + b\) có đồ thị như sau:

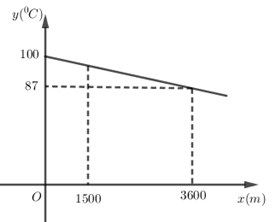
x: là đại lượng biểu thị cho độ cao so với mực nước biển.

y: là đại lượng biểu thị cho nhiệt độ sôi của nước.

Bài 7 (1 điểm) Năm học 2017 – 2018, trường THCS Tiến Thành có ba lớp 9 gồm 9A, 9B, 9C trong đó lớp 9A có 35 học sinh và lớp 9B có 40 học sinh. Tổng kết cuối năm, lớp 9A có 15 học sinh đạt danh hiệu học sinh giỏi, lớp 9B có 12 học sinh đạt danh hiệu học sinh giỏi, lớp 9C có 20% học sinh đạt danh hiệu học sinh giỏi và toàn khối 9 có 30% học sinh đạt danh hiệu học sinh giỏi. Hỏi lớp 9C có bao nhiêu học sinh?

Bài 8 (3 điểm).  Cho tam giác nhọn ABC có BC = 8 cm. Đường tròn tâm O đường kính BC cắt AB, AC lần lượt tại E và D. Hai đường thẳng BD và CE cắt nhau tại H.

a) Chứng minh: AH vuông góc với BC.

b) Gọi K là trung điểm của AH. Chứng minh tứ giác OEKD nội tiếp.

c) Cho \(\widehat {BAC} = {60^0}\). Tính độ dài đoạn DE và tỉ số diện tích của hai tam giác AED và ABC.

I. TRẮC NGHIỆM 

Chọn phương án trả lời đúng trong các câu sau:

Câu 1. Phương trình \({x^2} - 3x - 6 = 0\) có hai nghiệm \({x_1},\;\;{x_2}.\) Tổng \({x_1} + {x_2}\) bằng:

A. 3                                         B. -3

C. 6                                         D. -6

Câu 2. Đường thẳng \(y = x + m - 2\) đi qua điểm \(E\left( {1;\;0} \right)\) khi: 

A. \(m =  - 1\)                          B. \(m = 3\)

C. \(m = 0\)                             D. \(m = 1\)

Câu 3. Cho tam giác \(ABC\) vuông tại \(A,\;\;\widehat {ACB} = {30^0},\;\;AB = 5cm.\) Độ dài cạnh \(AC\) là:

A. \(10cm\)  

B. \(\dfrac{{5\sqrt 3 }}{2}cm\)   

C. \(5\sqrt 3 cm\)   

D. \(\dfrac{5}{{\sqrt 3 }}cm\) 

Câu 4. Hình vuông cạnh bằng 1, bán kính đường tròn ngoại tiếp hình vuông là:

 A. \(\dfrac{1}{2}\)  

B. \(1\)       

C. \(\sqrt 2 \)       

D. \(\dfrac{{\sqrt 2 }}{2}\) 

Câu 5. Phương trình \({x^2} + x + a = 0\) (với x là ẩn, a là tham số) có nghiệm kép khi:

A. \(a =  - \dfrac{1}{4}\)    

B. \(a = \dfrac{1}{4}\)         

C. \(a = 4\)    

D. \( - 4\)

Câu 6. Cho \(a > 0,\) rút gọn biểu thức \(\dfrac{{\sqrt {{a^3}} }}{{\sqrt a }}\) ta được kết quả:

A.\({a^2}\)

B. \(a\)

C. \( \pm a\)       

D. \( - a\) 

PHẦN II. TỰ LUẬN 

Câu 7. a) Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 5\\3x - y = 1\end{array} \right..\)

b) Tìm tọa độ giao điểm \(A,\;B\) của đồ thị hàm số \(y = {x^2}\) và \(y = x + 2.\) Gọi \(D,\;C\) lần lượt là hình chiếu vuông góc của \(A,\;B\) lên trục hoành. Tính diện tích tứ giác \(ABCD.\)

Câu 8. 

Nhân dịp Tết Thiếu nhi 01/06, một nhóm học sinh cần chia đều một số lượng quyển vở thành các phần quà để tặng cho các em nhỏ tại một mái ấm tình thương. Nếu mỗi phần quà giảm 2 quyển thì các em sẽ có thêm 2 phần quà nữa, còn nếu mỗi phần quà giảm 4 quyển thì các em sẽ có thêm 5 phần quà nữa. Hỏi ban đầu có bao nhiêu phần quà và mỗi phần quà có bao nhiêu quyển vở?

Câu 9 

Cho đường tròn đường kính AB, các điểm C, D nằm trên đường tròn đó sao cho C, D nằm khác phía đối với đường thẳng AB, đồng thời AD > AC. Gọi điểm chính giữa của các cung nhỏ AC và AD lần lượt là M, N; giao điểm của MN với AC, AD lần lượt là H, I; giao điểm của MD và CN là K.

a) Chứng minh \(\widehat {ACN} = \widehat {DMN}\). Từ đó suy ra tứ giác MCKH nội tiếp.

b) Chứng minh KH song song với AD.

c) Tìm hệ thức liên hệ giữa sđ cung AC và sđ cung AD để AK song song với ND.

Câu 10. a) Cho các số thực dương a, b, c thỏa mãn điều kiện \(a + b + c = 3\). Tìm giá trị nhỏ nhất của biểu thức \(A = 4{a^2} + 6{b^2} + 3{c^2}\)

b) Tìm các số nguyên dương a, b biết các phương trình \({x^2} - 2ax - 3b = 0\) và \({x^2} - 2bx - 3a = 0\) (với x là ẩn) đều có nghiệm nguyên.

Câu 1 

a) Tìm x để biểu thức \(A = \sqrt {2x - 1} \) có nghĩa.

b) Không sử dụng máy tính cầm tay, tính giá trị của biểu thức \(B = \sqrt 3 \left( {\sqrt {{3^2}.3}  - 2\sqrt {{2^2}.3}  + \sqrt {{4^2}.3} } \right).\)

c) Rút gọn biểu thức \(C = \left( {\dfrac{{\sqrt a }}{{\sqrt a  - 1}} - \dfrac{{\sqrt a }}{{a - \sqrt a }}} \right):\dfrac{{\sqrt a  + 1}}{{a - 1}}\) với \(a > 0\) và \(a \ne 1.\)

Câu 2 a) Giải phương trình \({x^4} + 3{x^2} - 4 = 0.\)

b) Cho đường thẳng \(d:\;y = \left( {m - 1} \right)x + n.\) Tìm các giá trị của \(m\) và \(n\) để đường thẳng \(d\) đi qua điểm \(A\left( {1;\; - 1} \right)\) và có hệ số góc bằng \( - 3.\)

Câu 3  Để phục vụ cho Festival Huế 2018, một cơ sở sản xuất nón lá dự kiến làm ra 300 chiếc nón lá trong một thời gian đã định. Do được bổ sung thêm nhân công nên mỗi ngày cơ sở đó làm ra được nhiều hơn 5 chiếc nón lá so với dự kiến ban đầu, vì vậy cơ sở sản xuất đã hoàn thành 300 chiếc nón lá sớm hơn 3 ngày so với thời gian đã định. Hỏi theo dự kiến ban đầu, mỗi ngày cơ sở đó làm được ra bao nhiêu chiếc nón lá? Biết rằng số chiếc nón lá làm ra mỗi ngày là bằng nhau và nguyên chiếc.

Câu 4  Cho phương trình \({x^2} + 2mx + {m^2} + m = 0\;\;\;\;\left( 1 \right)\) (với \(x\) là ẩn số).

a) Giải phương trình (1) khi \(m =  - 1.\)

b) Tìm giá trị của \(m\) để phương trình (1) có hai nghiệm phân biệt.

c) Tìm giá trị của \(m\) để phương trình (1) có hai nghiệm phân biệt \({x_1},\;{x_2}\) thỏa mãn điều kiện:\(\left( {{x_1} - {x_2}} \right)\left( {x_1^2 - x_2^2} \right) = 32.\)

Câu 5  Cho tam giác ABC cân tại A. Gọi M là điểm bất kì trên cạnh AC (M không trùng A và C). Một đường thẳng đi qua M cắt cạnh BC tại I và cắt đường thẳng AB tại N sao cho I là trung điểm của MN. Đường phân giác trong của góc BAC cắt đường tròn ngoại tiếp tam giác AMN tại điểm D (D không trùng A). Chứng minh rằng:

a) \(DN = DM\) và \(DI \bot MN\)

b) Tứ giác BNDI nội tiếp

c) Đường tròn ngoại tiếp tam giác AMN luôn đi qua một điểm cố định (khác điểm A) khi M di chuyển trên cạnh AC.

Bài 6 .  Cho hình chữ nhật ABCD với AB = 2a, BC = a. Khi quay hình chữ nhật ABCD quanh cạnh AB một vòng ta được hình trụ có thể tích V₁ và khi quay hình chữ nhật ABCD quanh cạnh BC một vòng thì được hình trụ có thể tích V₂. Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\)

Câu 1.Tính giá trị của các biểu thức sau:

\(\begin{array}{l}a)\;A = \sqrt {16 + 9}  - 2\\b)\;B = \sqrt {{{\left( {\sqrt 3  - 1} \right)}^2}}  + 1\end{array}\)  

Câu 2 .Cho biểu thức \(P = \left( {\frac{{x - 6}}{{x + 3\sqrt x }} - \frac{1}{{\sqrt x }} + \frac{1}{{\sqrt x  + 3}}} \right):\frac{{2\sqrt x  - 6}}{{x + 1}}\) với \(x > 0,\;\;x \ne 9.\)

a) Rút gọn biểu thức P.

b) Tìm giá trị của x để \(P = 1.\)

Câu 3 .1) Cho đường thẳng \(\left( d \right):\;\;y =  - \dfrac{1}{2}x + 2.\)

a) Tìm \(m\) để đường thẳng \(\left( \Delta  \right):\;y = \left( {m - 1} \right)x + 1\) song song với đường thẳng \(\left( d \right).\)

b) Gọi \(A,\;B\) là giao điểm của \(\left( d \right)\) với parabol \(\left( P \right):\;\;y = \dfrac{1}{4}{x^2}.\) Tìm tọa độ điểm \(N\) nằm trên trục hoành sao cho \(NA + NB\) nhỏ nhất.

2) Cho hệ phương trình: \(\left\{ \begin{array}{l}x + ay = 3a\\ - ax + y = 2 - {a^2}\end{array} \right.\;\;\;\left( I \right)\) với \(a\) là tham số.

a) Giải hệ phương trình (I) khi \(a = 1.\)

b) Tìm \(a\) để hệ phương trình (I) có nghiệm duy nhất \(\left( {x;\;y} \right)\) thỏa mãn \(\dfrac{{2y}}{{{x^2} + 3}}\) là số nguyên.

Câu 4 .Cho phương trình: \({x^2} - 2x + m - 3 = 0\;\;\;\left( 1 \right)\)  với \(m\) là tham số,

a) Giải phương trình \(\left( 1 \right)\) khi \(m = 0.\)

b) Tìm tất cả các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt \({x_1},\;\;{x_2}\) thỏa mãn:

\(x_1^2 + 12 = 2{x_2} - {x_1}{x_2}.\)

Câu 5 .

Cho đường tròn (O) đường kính AB = 2R, C là trung điểm OA và dây cung MN vuông góc với OA tại C. Gọi K là điểm tùy ý trên cung nhỏ BM (K khác B, M), H là giao điểm của AK và MN.

a) Chứng minh tứ giác BCHK là tứ giác nội tiếp.

b) Chứng minh \(AH.AK = A{M^2}\)

c) Xác định vị trí của điểm K để \(KM + KN + KB\) đạt giá trị lớn nhất và giá trị nhỏ nhất.

I. TRẮC NGHIỆM 

Học sinh chọn một phương án đúng nhất ở mỗi câu và viết phương án chọn vào bài làm:

Câu 1: Tìm x để biểu thức \(\dfrac{1}{{\sqrt {{{\left( {x - 2} \right)}^2}} }}\)  có nghĩa.

A. \(x \ge 2\)                            B. \(x > 2\)

C. \(x \ne  - 2\)                         D. \(x \ne 2\)

Câu 2:   Hàm số nào sau đây là hàm số bậc nhất?

A. \(y = ax + b\)        

B. \(y = 1 - 2x\)   

C. \(y = {x^2} + 1\)    

D. \(y = \dfrac{1}{x}\) 

Câu 3:  Cặp số nào sau đây không phải là nghiệm của phương trình \(x + 2y =  - 1?\)

A. \(\left( {1; - 1} \right)\)     

B. \(\left( { - 1;\;0} \right)\)         

C. \(\left( {0;\;\dfrac{1}{2}} \right)\)         

D. \(\left( {3; - 2} \right)\)  

Câu 4:  Hệ phương trình nào sau đây vô nghiệm?

A. \(\left\{ \begin{array}{l}y = 2x - 3\\y = x + 5\end{array} \right.\)                      

B. \(\left\{ \begin{array}{l}y = 2x - 3\\y = 2x + 1\end{array} \right.\)               

C. \(\left\{ \begin{array}{l}y = 2x - 3\\y = 4x - 6\end{array} \right.\)                        

D. \(\left\{ \begin{array}{l}y = 2x - 3\\y =  - x + 3\end{array} \right.\)

Câu 5: Cho hàm số \(y = a{x^2}\;\;\left( {a > 0} \right).\) Kết luận nào sau đây là đúng?

A. Hàm số đồng biến với mọi \(x.\)           

B. Hàm số nghịch biến với mọi \(x.\)             

C. Hàm số đồng biến khi \(x > 0.\)                 

D. Hàm số nghịch biến khi \(x > 0.\)

Câu 6:   Phương trình nào sau đây có hai nghiệm phân biệt?

A. \({x^2} + 3x - 4 = 0.\)                    

B. \({x^2} + 2x + 1 = 0\)                    

C. \({x^2} + x + 1 = 0\)                      

D. \({x^2} + 1 = 0\)

Câu 7: Cho tam giác ABC vuông tại A, đường cao AH. Biết AH = 2, HC = 4. Đặt BH = x. Tính x.

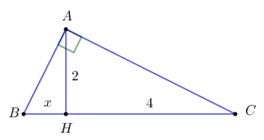
A. \(x = \dfrac{1}{2}\)                                 B. \(x = 1\)  

C. \(x = \dfrac{{16}}{3}\)                               D. \(x = 4\) 

Câu 8:  Cho tam giác ABC vuông tại A, đường cao AH. Đẳng thức nào sau đây là sai?

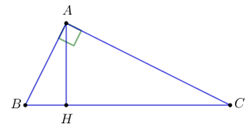
A. \(\sin B = \dfrac{{AH}}{{AB}}\)    

B. \(\tan \widehat {BAH} = \dfrac{{BH}}{{AH}}\)             

C. \(\cos C = \dfrac{{HC}}{{AC}}\)         

D. \(\cot \widehat {HAC} = \dfrac{{AH}}{{AC}}\) 

Câu 9:  Tính chu vi C của tam giác đều ABC ngoại tiếp đường tròn có bán kính bằng \(\sqrt 3 cm.\)

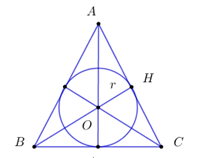
A. \(C = 9cm\)              

B. \(C = 9\sqrt 3 cm\)                                  

C. \(18cm\)              

D. \(18\sqrt 3 cm\) 

Câu 10:  Cho đường tròn tâm O đường kính 10cm. Gọi H là trung điểm của dây AB. Tính độ dài đoạn OH, biết AB = 6cm.

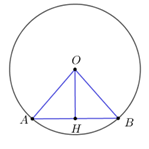
A. \(OH = 4cm\)                    

B. \(OH = 8cm\)

C. \(OH = 16cm\)                  

D. \(OH = 64cm\) 

Câu 11 :  Cho đường tròn \(\left( {O;\;6cm} \right)\) và đường tròn \(\left( {O';\;5cm} \right)\) có đoạn nối tâm \(OO' = 8cm.\)  Biết đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) cắt \(OO'\) lần lượt tại \(N,\;M.\) Tính độ dài \(MN.\) 

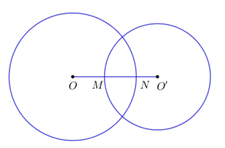
A. \(MN = 4cm\)                                

B. \(MN = 3cm\)

C. \(MN = 2cm\)                                     

D. \(MN = 1cm\)

Câu 12:  Cho tứ giác ABCD nội tiếp đường tròn tâm O. Khẳng định nào sau đây không đúng?

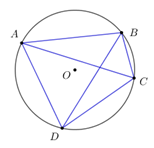
A. \(\widehat {ADC} = \widehat {CBA}\)                                       

B. \(\widehat {ADB} = \widehat {ACB}\) 

C. \(\widehat {ADC} + \widehat {ABC} = {180^0}\)

D. \(\widehat {DAB} + \widehat {DCB} = {180^0}\) 

II. TỰ LUẬN 

Câu 13 a) So sánh 5 và \(2\sqrt 6 \)

b) Giải phương trình \({x^4} - 4{x^2} - 5 = 0\)

Câu 14 

Cho phương trình \(4{x^2} - 2\left( {m + 1} \right)x + {m^2} = 0\,\) (m là tham số)

a) Với giá trị nào của m thì phương trình có nghiệm kép?

b) Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-ét, hãy tính tổng các bình phương hai nghiệm của phương trình.

Câu 15 .Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Nếu mở cả hai vòi nước chảy vào một bể cạn thì sau 3 giờ bể đầy nước. Nếu mở riêng từng vòi thì vòi thứ nhất làm đầy bể nhanh hơn vòi thứ hai là 2 giờ 30 phút. Hỏi nếu mở từng vòi thì mỗi vòi chảy bao lâu đầy bể.

Câu 16 

Cho đường tròn \(\left( {O;R} \right)\) đường kính AB. Gọi d là tiếp tuyến của đường tròn tại A, C là điểm chuyển động trên đường thẳng d. BC cắt (O) tại D \(\left( {D \ne B} \right)\). Gọi E là trung điểm của BD.

a) Chứng minh OACE là tứ giác nội tiếp.

b) Chứng minh rằng \(BE.BC = 2{R^2}\)

c) Tìm tập hợp các tâm I của đường tròn ngoại tiếp tam giác ACE.

Câu 1 .

a) Rút gọn biểu thức: \(P = 3\sqrt 5  + \sqrt {20} .\)

b) Giải hệ phương trình: \(\left\{ \begin{array}{l}x + 2y = 5\\x - y = 2\end{array} \right..\)

c) Tìm giá trị của tham số m để đồ thị hàm số \(y = x + m\) đi qua điểm \(A\left( {0;\;3} \right).\)

Câu 2 

Cho phương trình \({x^2} - mx + m - 4 = 0\;\;\left( 1 \right),\)  (x là ẩn số và m là tham số).

a) Giải phương trình (1) khi \(m = 8.\)

b) Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) với mọi \(m.\) Tìm tất cả các giá trị nguyên dương của \(m\) để \(\left( {5{x_1} - 1} \right)\left( {5{x_2} - 1} \right) < 0.\)

Câu 3 (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.

Một hình chữ nhật có chu vi bằng 28 cm. Tính chiều dài và chiều rộng của hình chữ nhật, biết rằng nếu tăng chiều dài thêm 1 cm và tăng chiều rộng thêm 2 cm thì diện tích của hình chữ nhật đó tăng thêm 25 cm².

Câu 4

Cho tam giác ABC nhọn có AB < AC và đường cao AK. Vẽ đường tròn tâm O đường kính BC. Từ A kẻ các tiếp tuyến AM, AN với đường tròn (O) (M, N là các tiếp điểm, M và B nằm trên cùng nửa mặt phẳng có bờ là đường thẳng AO). Gọi H là giao điểm của hai đường thẳng MN và AK. Chứng minh rằng:

a) Tứ giác AMKO nội tiếp đường tròn.

b) KA là tia phân giác của góc MKN.

c) \(A{N^2} = AK.AH\)

d) H là trực tâm tam giác ABC.

Bài 5

Cho a, b là hai số thực dương thỏa mãn \(a + b \le 4\). Tìm giá trị nhỏ nhất của biểu thức \(S = \dfrac{1}{{{a^2} + {b^2}}} + \dfrac{{25}}{{ab}} + ab\)

Câu 1 Rút gọn biểu thức:

a) \(A = \sqrt {45}  + \sqrt {20}  - 2\sqrt 5 .\)

b) \(B = \dfrac{{a + 2\sqrt a }}{{\sqrt a  + 2}} - \dfrac{{a - 4}}{{\sqrt a  - 2}}\) (với \(a \ge 0,\;\;a \ne 4\)).

Câu 2 

a) Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 4\\2x - y = 5\end{array} \right..\)

b) Cho hàm số \(y = \dfrac{1}{2}{x^2}\) có đồ thị \(\left( P \right)\) và đường thẳng \(d:\;y = x - 2m.\) Vẽ đồ thị \(\left( P \right).\) Tìm tất cả các giá trị của \(m\) sao cho \(d\) cắt \(\left( P \right)\) tại điểm có hoành độ bằng \( - 1.\)

Câu 3  Cho phương trình \({x^2} + 4x + m + 1 = 0\,\,\,(1)\) (với m là tham số).

a) Giải phương trình (1) với m = 2.

b) Tìm điều kiện của m để phương trình (1) có nghiệm.

c) Tìm tất cả các giá trị của m sao cho phương trình (1) có hai nghiệm \({x_1};{x_2}\) thỏa mãn điều kiện \(\dfrac{{{x_1} - 1}}{{2{x_2}}} - \dfrac{{{x_2} - 1}}{{2{x_1}}} =  - 3\).

Câu 4: Cho nửa đường tròn tâm O đường kính AB. Vẽ bán kính CO vuông góc với AB, M là một điểm bất kỳ trên cung AC (M khác A, C và điểm chính giữa AC), BM cắt AC tại H. Gọi K là chân đường vuông góc kẻ từ H đến AB.

a) Chứng minh tứ giác BCHK là tứ giác nội tiếp

b) Chứng minh CA là phân giác của góc MCK

c) Kẻ CP vuông góc với BM \(\left( {P \in BM} \right)\) và trên đoạn thẳng BM lấy điểm E sao cho BE = AM. Chứng minh ME = 2CP

I. PHẦN TRẮC NGHIỆM:

Câu 1: Tam giác MNP đều, nội tiếp đường tròn (O; R), khi đó số đo \(\widehat {NOP}\) là:

A. \({150^0}\)                     

B. \({60^0}\)               

C. \({30^0}\)              

D. \({120^0}\)

Câu 2:   Phương trình nào sau đây có hai nghiệm trái dấu?

A. \({x^2} - 2017x - 2018 = 0\)         

B. \({x^2} - 2018x + 2017 = 0\)              

C. \( - {x^2} + 2017x - 2018 = 0\)          

D. \({x^2} - 2019x + 2018 = 0\) 

Câu 3:  Tìm m để hàm số \(y = \dfrac{3}{{m + 2}}x + 1\) đồng biến trên tập số thực \(R.\) 

A. \(m >  - 2\)          

B. \(m <  - 2\)       

C. \(m > 2\)             

D. \(m \le  - 2\) 

Câu 4:  Biết \(\left( {a;\;b} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x - 3y = 2\\x + y = 4\end{array} \right..\) Khi đó giá trị của biểu thức \(2{a^2} - {b^2}\)  là:

A. 4                                         B. -12          

C. -4                                        D. 8

Câu 5: Giá trị của biểu thức \(\sin {62^0} - \cos {28^0}\) bằng:

A. 0        

B. 1      

C. \(2\sin {62^0}\)

D. \(2\cos {28^0}\)

Câu 6:   Hệ số góc của đường thẳng \(y =  - 5x + 7\) là:

A. \( - 5x\)                   

B. \(5\)             

C. \( - 5\)                

D. \(7\) 

Câu 7: Cho tam giác \(ABC\) vuông tại \(C.\) Biết \(\sin B = \dfrac{1}{3},\) khi đó \(\tan A\) bằng:

A. \(\dfrac{{2\sqrt 2 }}{3}\)        

B. \(3\)          

C. \(2\sqrt 2 \)           

D. \(\dfrac{1}{{2\sqrt 2 }}\) 

Câu 8:  Cho hai đường tròn \(\left( {O;\;4cm} \right)\) và đường tròn \(\left( {I;\;2cm} \right),\) biết \(OI = 6cm.\) Số tiếp tuyến chung của hai đường tròn đó là:

A. 4                                         B. 3          

C. 2                                         D. 1

Câu 9:  Kết quả của phép tính \(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}}  - \sqrt 5 \) là:

A. \(2\sqrt 5  - 2\)                 

B. \( - 2\)                          

C. \(2\)                     

D. \(2 - 2\sqrt 5 \) 

Câu 10:  Tìm m để hai đường thẳng \(\left( d \right):\;\;y = 3x + 1\) và \(\left( {d'} \right):\;\;y = \left( {m - 1} \right)x - 2m\) song song với nhau.

A. \(m =  - \dfrac{1}{2}\)      

B. \(m = 4\)     

C. \(m =  - \dfrac{3}{2}\)       

D. \(m \ne 4\) 

Câu 11:  Từ một miếng tôn có hình dạng là nửa hình tròn bán kính 1m, người ta cắt ra một hình chữ nhật (phần tô đậm như hình vẽ). Phần hình chữ nhật có diện tích lớn nhất có thể cắt được là: 

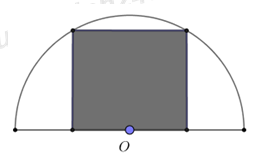
A. \(1,6{m^2}\)               

B. \(0,5{m^2}\)                                  

C. \(1{m^2}\)           

D. \(2{m^2}\) 

Câu 12: Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AC\), có \(\widehat {BAC} = {60^0}\) (hình vẽ). Khi đó số đo của \(\widehat {ADB}\) là:

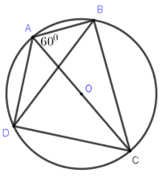
A. \({45^0}\)               B. \({60^0}\)   

C. \({40^0}\)               D. \({30^0}\).

Câu 13:  Một hình cầu có đường kính 6cm. Diện tích mặt cầu đó là: 

A. \(36\pi c{m^2}\)           

B. \(12\pi c{m^2}\)           

C. \(216\pi c{m^2}\)     

D. \(72\pi c{m^2}\) 

Câu 14: Cặp số nào sau đây là một nghiệm của phương trình \(x - 3y =  - 1?\)

A. \(\left( {2;\;0} \right)\)         

B. \(\left( {2;\;1} \right)\)     

C. \(\left( {1;\;2} \right)\)          

D. \(\left( {2;\; - 1} \right)\)

Câu 15: Trên cùng mặt phẳng tọa độ Oxy cho ba đường thẳng \(y = x + 2;\;y = 2x + 1\) và \(y = \left( {{m^2} - 1} \right)x - 2m + 1.\) Tìm giá trị của m để ba đường thẳng cùng đi qua một điểm.

A. \(m =  - 3\)           

B. \(m \in \left\{ { - 3;\;1} \right\}\)       

C. \(m \in \left\{ { - 1;\;3} \right\}\)        

D. \(m = 1\) 

Câu 16: Trong mặt phẳng tọa độ Oxy, tập nghiệm của phương trình \(4x + y = 1\) được biểu diễn bởi đồ thị hàm số nào dưới đây?

A. \(y = 4x + 1\)            

B.  \(y =  - 4x - 1\)         

C. \(y =  - 4x + 1\)

D. \(y = 4x - 1\) 

Câu 17: Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(BH = 3,2cm;\;\;BC = 5cm\) thì độ dài \(AB\)  bằng:

A. \(8cm\)                                B. -\(16cm\)

C. \(1,8cm\)                             D. \(4cm\) 

Câu 18: Biết phương trình \(3{x^2} + 6x - 9 = 0\) có hai nghiệm \({x_1};{x_2}\). Giả sử \({x_1} < {x_2}\) khi đó biểu thức \(\dfrac{{{x_2}}}{{{x_1}}}\) có giá trị là:

A. \(\dfrac{1}{3}\)        

B. \( - \dfrac{1}{3}\)        

C. \( - 3\)            

D. 3

Câu 19: Cho các đường tròn \(\left( {A;3cm} \right);\,\,\left( {B;\;5cm} \right);\,\,\left( {C;2cm} \right)\) đôi một tiếp xúc ngoài với nhau. Chu vi của \(\Delta ABC\) là:

A. 20cm                 

B. \(10\sqrt 2 cm\)          

C. 10cm               

D. \(10\sqrt 3 cm\)

Câu 20: Điều kiện xác định của biểu thức \(\sqrt {x - 15} \) là:

A. \(x \le  - 15\)        

B. \(x \ge 15\)      

C. \(x \ge  - 15\)          

D. \(x \le 15\)

Câu 21: Kết quả rút gọn biểu thức \(\dfrac{1}{{\sqrt {13}  + \sqrt {15} }} + \dfrac{1}{{\sqrt {15}  + \sqrt {17} }}\) là:

A. \(\dfrac{{\sqrt {13}  - \sqrt {17} }}{2}\)

B. \(\dfrac{{\sqrt {17}  + \sqrt {13} }}{2}\)      

C. \(\sqrt {17}  - \sqrt {13} \)         

D. \(\dfrac{{\sqrt {17}  - \sqrt {13} }}{2}\)

Câu 22: Đổ nước vào một chiếc thùng hình trụ có bán kính 20cm. Nghiêng thùng sao cho mặt nước chạm miệng thùng và đáy thùng (như hình vẽ) thì mặt nước tạo với đáy thùng một góc 45⁰. Thể tích của thùng là:

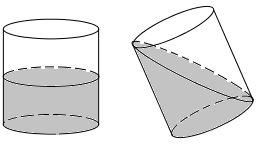
A. \(400\pi \,\,\left( {c{m^3}} \right)\)                        

B. \(32000\pi \,\left( {c{m^3}} \right)\)

C. \(16000\pi \,\left( {c{m^3}} \right)\)                      

D. \(8000\pi \,\left( {c{m^3}} \right)\)

Câu 23: Cho hai đường thẳng \(\left( {{d_1}} \right):\,\,y =  - 2x + 3\) và \(\left( {{d_2}} \right):\,\,y =  - \dfrac{1}{2}x + 3\). Khẳng định nào sau đây là đúng?

A. (d₁) và (d₂) trùng nhau       

B. (d₁) và (d₂) cắt nhau tại một điểm trên trục trung

C. (d₁) và (d₂) song song với nhau  

D. (d₁) và (d₂) cắt nhau tại một điểm trên trục hoành.

Câu 24: Số nhà của bạn Nam là một số tự nhiên có hai chữ số. Nếu thêm chữ số 7 vào bên trái số đó thì được một số kí hiệu là A. Nếu thêm chữ số 7 vào bên phải chữ số đó thì được một số kí hiệu là B. Tìm số nhà của bạn Nam biết \(A - B = 252\).

A. 45                                       B. 54     

C. 90                                       D. 49

Câu 25: Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\left( d \right):\,\,y = x - m + 2\) và parabol: \(\left( P \right):\,\,y = {x^2}\). Tìm m để (d) và (P) cắt nhau tại hai điểm phân biệt nằm trên cùng một nửa mặt phẳng có bờ là trục tung:

B. \(\dfrac{4}{9} < m < 2\)       

C. \(2 < m < \dfrac{9}{4}\)        

D. \(m < \dfrac{4}{9}\)

II. PHẦN TỰ LUẬN: 45 PHÚT

Câu 1 .

a) Rút gọn biểu thức \(P = \sqrt 3 \left( {\sqrt {12}  - 3} \right) + \sqrt {27} \)

b) Tìm giá trị của m để đồ thị hàm số \(y = m{x^2}\) đi qua điểm \(A\left( {2;4} \right)\).

c) Giải phương trình \({x^2} - 6x + 5 = 0\)

Câu 2 .Cho hệ phương trình \(\left\{ \begin{array}{l}3x - y = 2m + 3\\x + 2y = 3m + 1\end{array} \right.\) (m là tham số)

a) Giải hệ phương trình khi \(m = 2\).

b) Tìm m để hệ phương trình có nghiệm \(\left( {x;y} \right)\) thỏa mãn điều kiện \({x^2} + {y^2} = 5\).

Câu 3  Cho đường tròn (O) đường kính AB và một dây CD vuông góc với AB tại H (H không trừng với các điểm A, B, O). Gọi M là trung điểm của AD. Chứng minh:

a) Bốn điểm O, M, D, H cùng thuộc một đường tròn.

b) MH vuông góc với BC.

Câu 4 
Cho x, y, z là 3 số thực dương thỏa mãn \({x^2} + {y^2} + {z^2} = 2\). Tìm giá trị lớn nhất của biểu thức  

\(A = \dfrac{2}{{{x^2} + {y^2}}} + \dfrac{2}{{{y^2} + {z^2}}} + \dfrac{2}{{{z^2} + {x^2}}}\)\(\, - \dfrac{{{x^3} + {y^3} + {z^3}}}{{2xyz}}\)

Bài 1. Giải các phương trình và hệ phương trình sau đây

a. \(\sqrt 3 x - \sqrt 2 x = \sqrt 3  + \sqrt 2 \)       

b. \(\left\{ \begin{array}{l}x + y = 101\\ - x + y =  - 1\end{array} \right.\)

c. \({x^2} + 2\sqrt 3 x + 2 = 0\)

Bài 2.  Cho hàm số \(y = 0,5.{x^2}\) có đồ thị là Parabol (P)

a.Vẽ đồ thị (P) của hàm số đã cho

b.Xác định hệ số a; b của đường thẳng (d): \(y = ax + b\) , biết (d) cắt trục hoành tại điểm có hoành độ bằng 1 và (d) cắt (P) tại điểm có hoành độ bằng 2. Chứng tỏ (P) và (d) tiếp xúc nhau.

Bài 3.  Cho phương trình bậc hai \({x^2} - 3x + m = 0\) (m là tham số).

a.Tìm m để phương trình có nghiệm bằng \( - 2\) . Tính nghiệm còn lại ứng với m vừa tìm được.

b.Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình đã cho. Tìm giá trị nhỏ nhất của \(A = x_1^2 + x_2^2 - 3{x_1}{x_2}\)

Bài 4.  Cho tam giác đều ABC nội tiếp trong đường tròn tâm O. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA.

a.Chứng minh tứ giác BMON nội tiếp được đường tròn.

b.Kéo dài AN cắt đường tròn (O) tại G (khác A). Chứng minh ON = NG.

b.PN cắt cung nhỏ BG  của đường tròn (O) tại điểm F. Tính số đo của góc \(\widehat {OFP}\) .

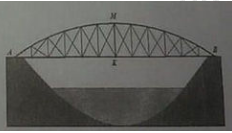
Bài 5  Cầu vòm là một dạng cầu đẹp bởi hình dáng cầu được uốn lượn theo một cung tròn tạo sự hài hòa trong thiết kế cảnh quan, đặc biệt là các khu đô thị có dòng sông chảy qua, tạo được một điểm nhấn của công trình giao thông hiện đại. Một chiếc cầu vòm được thiết kế như hình vẽ bên, vòm cầu là một cung tròn AMB. Độ dài đoạn AB bằng 30m, khoảng cách từ vị trí cao nhất ở giữa vòm cầu so với sàn mặt cầu là đoạn MK có độ dài 5m. Tính chiều dài vòm cầu.

Bài 1. a) Trục căn thức ở mẫu của biểu thức \(A = \dfrac{1}{{2 - \sqrt 3 }}\)

b) Cho \(a \ge 0,a \ne 4.\) Chứng minh \(\dfrac{{\sqrt a }}{{\sqrt a  + 2}} + \dfrac{{2\left( {\sqrt a  - 2} \right)}}{{a - 4}} = 1\) .

Bài 2. 

a) Giải hệ phương trình: \(\left\{ \begin{array}{l}x + 2y = 14\\2x + 3y = 24\end{array} \right.\)   

b) Giải phương trình \(4x + \dfrac{3}{{x - 1}} = 11\)

Bài 3. 

Vẽ đồ thị của các hàm số \(y =  - \dfrac{1}{2}{x^2}\)  và \(y = x - 4\)  trên cùng một mặt phẳng tọa độ. Gọi A và B là các giao điểm của đồ thị hai hàm số trên. Tính bán kính của đường tròn ngoại tiếp tam giác OAB, với O là gốc tọa độ (đơn vị đo trên các tọa độ là centimet).

Bài 4 Cho  phương trình \({x^2} + 2\left( {m - 1} \right)x + 4m - 11 = 0,\) với \(m\) là tham số. Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\;{x_2}\) thỏa mãn hệ thức \(2{\left( {{x_1} - 1} \right)^2} + \left( {6 - {x_2}} \right)\left( {{x_1}{x_2} + 11} \right) = 72.\)

Bài 5

Cạnh huyền của một tam giác vuông bằng 17 cm. Hai cạnh góc vuông có độ dài hơn kém nhau 7 cm. Tính diện tích của tam giác vuông đó.

Bài 6

Cho tam giác nhọn ABC nội tiếp trong đường tròn tâm O có AB < AC. Trên cung nhỏ AC lấy điểm M khác A thỏa mãn MA < MC. Vẽ đường kính MN của đường tròn (O) và gọi H, K lần lượt là hình chiếu vuông góc của A trên MB, MN. Chứng minh rằng:

a) Bốn điểm A, H, K, M cùng nằm trên một đường tròn.

b) AH.AK = HB.MK.

c) Khi điểm M di động trên cung nhỏ AC thì đường thẳng HK luôn qua một điểm cố định.

Câu I 

1) a) Rút gọn: \(A = \sqrt {12}  + \sqrt 3 .\)

    b) Tìm \(x\) biết \(4x - 6 = 0.\)

2) a) Rút gọn biểu thức: \(B = {\left( {x + 2} \right)^2} - {x^2}.\)

    b) Vẽ đồ thị hàm số \(y = 2x - 3\) trong mặt phẳng tọa độ \(Oxy.\)

Câu II :

1) Giải phương trình: \({x^4} - 8{x^2} - 9 = 0.\)

2) Giải hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{2}{{y + 1}} = 4\\\dfrac{2}{x} - \dfrac{1}{{y + 1}} = 3\end{array} \right..\)

Câu III 

1)  Do cải tiến kỹ thuật nên tổng sản lượng thu hoạch cam nhà bác Minh  năm 2017 đạt 180 tấn, tăng 20%  so với năm 2016. Hỏi năm 2016 nhà bác Minh thu hoạch được bao nhiêu tấn cam?

2)  Cho hình chữ nhật ABCD, kẻ AH vuông góc với BD tại H, đường thẳng AH cắt DC tại E, biết AH = 4cm, HE = 2cm. Tính diện tích hình chữ nhật ABCD.

Câu IV:

Cho đường tròn \(\left( {O;R} \right)\) đường kính AB, một dây CD cắt đoạn thẳng AB tại E, tiếp tuyến của (O) tại B cắt các tia AC, AD lần lượt tại M, N.

1)  Chứng minh rằng \(\angle ACD = \angle ANM\)

2)  Chứng minh rằng \(AC + AD + AM + AN > 8R\)

Câu V.

1) Giải phương trình: \({x^2} + 2 = 2\sqrt {{x^3} + 1} .\)

2) Cho x, y là các số không âm thỏa mãn \(x + y = 4\). Chứng minh \({x^2}{y^2}\left( {{x^2} + {y^2}} \right) \le 128\)

Câu 1. 

a)  Giải phương trình: \(3x - 2 = 0\)

b)  Giải phương trình \({x^2} - 5x + 6 = 0\)

c)  Giải hệ phương trình: \(\left\{ \begin{array}{l}2x - 3y = 1\\x - 2y =  - 1\end{array} \right.\)

d)     Quãng sông từ A đến B dài \(60km\) . Một ca nô xuôi dòng từ A  đến B rồi ngược từ B trở về A mất tổng cộng 8 giờ. Tính vận tốc thực của ca nô, biết vận tốc dòng nước là \(4km/h.\) 

Câu 2. Rút gọn các biểu thức:

a)  \(A = 2\sqrt {20}  + 3\sqrt {45}  - 4\sqrt {80} .\)

b)  \(B = \left( {2 + \dfrac{1}{{\sqrt x  - 1}}} \right).\dfrac{{x - 1}}{{2\sqrt x  - 1}}\)\(\,\,\,\left( {x \ge 0;x \ne 1;x \ne \dfrac{1}{4}} \right).\)

Câu 3. 

a) Vẽ Parabol (P): \(y = 2{x^2}\) trên mặt phẳng tọa độ Oxy.

b) Tìm a, b để đường thẳng (d): \(y = ax + b\) đi qua \(M\left( {0; - 1} \right)\)  và tiếp xúc với Parabol (P).

Câu 4.  Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + 6m - 4 = 0\,\,\,\left( 1 \right)\) (với m là tham số)

a)  Chứng minh rằng phương trình (1) luôn có hai nghiệm phân biệt với mọi m.

b)  Tìm m để phương trình (1) có hai nghiệm \({x_1};x {  _2}\)  thỏa mãn:

\(\left( {2m - 2} \right){x_1} + x_2^2 - 4{x_2} = 4.\)

Câu 5  Cho đường tròn \(\left( O \right)\) đường kính \(AB.\) Kẻ tiếp tuyến \(Ax\) với đường tròn \(\left( O \right).\) Trên tia \(Ax\) lấy điểm \(C,\) từ điểm \(C\) vẽ đường thẳng cắt đường tròn \(\left( O \right)\) tại hai điểm \(D\) và \(E\) (\(D,\;\;E\) không cùng nằm trên nửa mặt phẳng bờ \(AB;\;D\) nằm giữa \(C\) và \(E\)). Từ điểm \(O\) kẻ \(OH \bot DE = \left\{ H \right\}.\)

a) Chứng minh rằng tứ giác \(AOHC\) nội tiếp.

b) Chứng minh rằng \(AD.CE = AC.AE.\)

c) Đường thẳng \(CO\) cắt tia \(BD,\) tia \(BE\) lần lượt tại \(M\) và \(N.\) Chứng minh rằng tứ giác \(AMBN\) là hình bình hành.

Bài I (2,0 điểm) Cho hai biểu thức \(A = \dfrac{{\sqrt x  + 4}}{{\sqrt x  - 1}}\) và \(B = \dfrac{{3\sqrt x  + 1}}{{x + 2\sqrt x  - 3}} - \dfrac{2}{{\sqrt x  + 3}}\) với \(x \ge 0,x \ne 1\)

1) Tính giá trị của biểu thức A khi \(x = 9\)

2) Chứng minh \(B = \dfrac{1}{{\sqrt x  - 1}}\)

3) Tìm tất cả các giá trị của x để \(\dfrac{A}{B} \ge \dfrac{x}{4} + 5\)

Bài II. (2,0 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:

Một mảnh đất hình chữ nhật có chu vi bằng 28 mét và độ dài đường chéo bằng 10 mét. Tính chiều dài và chiều rộng của mảnh đất đó theo đơn vị mét.

Bài III 

1) Giải hệ phương trình \(\left\{ \begin{array}{l}4x - \left| {y + 2} \right| = 3\\x + 2\left| {y + 2} \right| = 3\end{array} \right.\)

2) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): \(y = \left( {m + 2} \right)x + 3\) và Parabol \(\left( P \right)\,:\,y = {x^2}\)

a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt.

b) Tìm tất cả các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có các hoành độ là các số nguyên.

Bài IV. 

Cho đường tròn (O;R) với dây cung AB không đi qua tâm. Lấy S là một điểm bất kì trên tia đối của tia AB (S khác A). Từ điểm S vẽ hai tiếp tuyến SC, SD với đường tròn (O;R) sao cho điểm C nằm trên cung nhỏ AB (C, D là các tiếp điểm). Gọi H là trung điểm của đoạn thẳng AB.

1) Chứng minh năm điểm C, D, H, O, S thuộc đường tròn đường kính SO.

2) Khi SO = 2R, hãy tính độ dài đoạn thẳng SD theo R và tính số đo \(\widehat {CSD}\) .

3) Đường thẳng đi qua điểm A và song song với đường thẳng SC, cắt đoạn thẳng CD tại điểm K. Chứng minh tứ giác ADHK là tứ giác nội tiếp và đường thẳng BK đi qua trung điểm của đoạn thẳng SC.

4) Gọi E là trung điểm của đoạn thẳng BD và F là hình chiếu vuông góc của điểm E trên đường thẳng AD. Chứng minh rằng, khi điểm S thay đổi trên tia đối của tia AB thì điểm F luôn thuộc một đường tròn cố định.

Bài V  Tìm giá trị nhỏ nhất của biểu thức \(P = \sqrt {1 - x}  + \sqrt {1 + x}  + 2\sqrt x \)

Câu 1.

a)  Giải phương trình: \({x^2} + x - 12 = 0.\)

b)  Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 6\\2x + y = 2\end{array} \right.\)

Câu 2  Cho parabol: \(y = 3{x^2}\) và đường thẳng \(d:\,\,y = x + m - 1\) (với m là tham số).

a)  Vẽ parabol (P).

b)  Tìm tất cả các giá trị của m để (P) cắt (d) tại đúng một điểm.

Câu 3 . Một mảnh vườn hình chữ nhật có chiều dài hơn chiều rộng 5m. Nếu tăng chiều dài thêm 10m và chiều rộng thêm 5m thì diện tích mảnh vườn đó tăng gấp đôi. Tính chiều dài và chiều rộng mảnh vườn đó.

Câu 4 . Cho tam giác ABC vuông tại A, M là trung điểm của cạnh AC. Vẽ đường tròn đường kính MC cắt cạnh BC tại N \(\left( {N \ne C} \right).\) Đường thẳng BM cắt đường tròn đường kính MC tại D \(\left( {D \ne M} \right).\) Chứng minh:

a)  Tứ giác BADC nội tiếp được trong một đường tròn. Xác định tâm O của đường tròn đó.

b)  \(CM.CA = CN.CB.\)

c)  \(O{M^2} = ON.OC.\)

Câu 5 . Cho hai số dương x, y thỏa mãn \(xy = 2018.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{2}{x} + \dfrac{{1009}}{y} - \dfrac{{2018}}{{2018x + 4y}}.\)

Câu 1.

1. Giải các phương trình sau:

a) \(5\left( {x + 1} \right) = 3x + 7\)               

b) \({x^4} - {x^2} - 12 = 0\)

2. Cho hệ phương trình: \(\left\{ \begin{array}{l}3x - y = 2m - 1\\x + 2y = 3m + 2\end{array} \right.\)

a) Giải hệ phương trình khi \(m = 1\)              b) Tìm m để hệ có nghiệm \(\left( {x;y} \right)\) thỏa mãn: \({x^2} + {y^2} = 10\)

Câu 2. Cho phương trình \(A = \left( {\dfrac{1}{{x - \sqrt x }} + \dfrac{1}{{\sqrt x  - 1}}} \right):\dfrac{{\sqrt x  + 1}}{{{{\left( {\sqrt x  - 1} \right)}^2}}}\) (với \(x > 0,x \ne 1\) )

a) Rút gọn biểu thức A.       

b) Tìm giá trị lớn nhất của biểu thức \(P = A - 9\sqrt x \)

Câu 3. Một chiếc bè trôi từ bến sông A đến bên B với vận tốc dòng nước là 4km/h, cùng lúc đó một chiếc thuyền chạy từ bến A đến B rồi quay lại ngay thì gặp chiếc bè tại vị trí C cách bến A là 8km. Tính vận tốc thực của thuyền biết khoảng cách giữa hai bến A và B là 24 km.

Câu 4.. Trong hệ tọa độ Oxy, cho Parabol \(y = {x^2}\left( P \right)\) và đường thẳng có phương trình \(y = \left( {m - 1} \right)x + {m^2} - 2m + 3\left( d \right)\)

a) Chứng minh với mọi giá trị của m thì (d) luôn cắt (P) tại hai điểm phân biệt.

b) Giả sử (d) cắt (P) tại hai điểm phân biệt A, B. Tìm m để tam giác OAB cân tại O. Khi đó tính diện tích tam giác OAB.

Câu 5.  Cho nửa đường tròn tâm O đường kính AB, M là một điểm bất kỳ thuộc nửa đường tròn (M khác A, B). Tiếp tuyến tại M cắt các tiếp tuyến Ax và By của nửa đường tròn đó lần lượt tại C và D.

a) Chứng minh: \(\widehat {COD} = {90^0}\)

b) Gọi K là giao điểm của BM với Ax. Chứng minh: \(\Delta KMO \sim \Delta AMD\)

c) Tìm giá trị nhỏ nhất của tổng diện tích hai tam giác ACM và BDM.

Câu 6. 

a) Cho hàm số \(y = f\left( x \right)\)  với \(f\left( x \right)\) là một biểu thức đại số xác định với mọi số thực \(x \ne 0\) . Biết rằng: \(f\left( x \right) + 3f\left( {\dfrac{1}{x}} \right) = {x^2}\left( {\forall x \ne 0} \right).\) Tính \(f\left( 2 \right)\)

b) Cho ba số nguyên dương \(a,b,c\) đôi một khác nhau và thỏa mãn: \(a\) là ước của \(b + c + bc\), \(b\)  là ước của \(c + a + ca\)  và \(c\) là ước của \(a + b + ab\) . Chứng minh \(a,b,c\) không đồng thời là các số nguyên tố.

Câu 1: Đồ thị ở hình bên là đồ thị hàm số nào trong các hàm số sau:

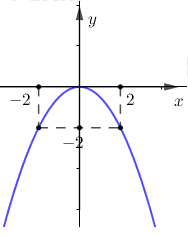
A. \(y =  - 2{x^2}\)

B. \(y =  - \dfrac{1}{4}{x^2}\)

C. \(y =  - 4{x^2}\)

D. \(y =  - \dfrac{1}{2}{x^2}\)

Câu 2. Tìm điều kiện của x để đẳng thức \(\sqrt {\dfrac{{x + 2}}{{x - 3}}}  = \dfrac{{\sqrt {x + 2} }}{{\sqrt {x - 3} }}\) đúng.

A. \(x > 2\)

B. \(x \ge  - 2\)

C. \(x \ge  - 3\)

D. \(x > 3\)

Câu 3. Độ dài hai cạnh của một tam giác là 2 (cm) và 21 (cm). Số đo nào dưới đây có thể là độ dài cạnh thứ ba của tam giác đã cho?

A. 19 (cm)

B. 22 (cm)

C. 23(cm)

D. 24 (cm)

Câu 4. Tìm các giá trị của a sao cho \(\dfrac{{a - 1}}{{\sqrt a }} < 0.\)

A. \(a \ge 0\)

B. \(0 \le a < 1\)

C. \(a < 1\)

D. \(0 < a < 1\)

Câu 5. Cho số tự nhiên \(\overline {10203x} \) . Tìm tất cả các chữ số x thích hợp để số đã cho chia hết cho 3 mà không chia hết cho 9?

A. \(x \in \left\{ {0;6;9} \right\}\)

B. \(x \in \left\{ {0;3;6} \right\}\)

C. \(x \in \left\{ {3;6;9} \right\}\)

D. \(x \in \left\{ {0;3;9} \right\}\)

Câu 6. Biết phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có một nghiệm x = 1. Đẳng thức nào sau đây đúng ?

A. \(a - b - c = 0.\)

B. \(a + b - c = 0.\)

C. \(a + b + c = 0.\)

D. \(a - b + c = 0.\)

Câu 7. Xác định hàm số \(y = ax + b,\) biết đồ thị của hàm số đi qua hai điểm \(A\left( { - 2;5} \right)\) và \(B\left( {1; - 4} \right)\)

A. \(y = x - 3\)

B. \(y =  - x - 3\)

C.  \(y =  - 3x - 1\)

D. \(y = 3x - 1\)

Câu 8. Trong các phân số sau, phân số nào viết dưới dạng số thập phân vô hạn tuần hoàn?

A. \(\dfrac{{17}}{{20}}.\)

B. \(\dfrac{7}{{55}}.\)

C. \(\dfrac{{19}}{{128}}.\)

D. \(\dfrac{{67}}{{625}}.\)

Câu 9.Tìm tất cả các giá trị của m để đồ thị hàm số \(y = \left( {2m + 1} \right){x^2}\) nằm phía dưới trục hoành.

A. \(m <  - \dfrac{1}{2}\)

B. \(m >  - \dfrac{1}{2}\)

C. \(m \ge  - \dfrac{1}{2}\)

D. \(m \le  - \dfrac{1}{2}\)

Câu 10: Phương trình \(\dfrac{3}{{1 - 4x}} = \dfrac{2}{{4x + 1}} - \dfrac{{8 + 6x}}{{16{x^2} - 1}}\) có bao nhiêu nghiệm?

A. 2

B. 0

C. 1

D. 3

Câu 11. Đẳng thức nào sau đây đúng với mọi \(x \le 0?\)

A. \(\sqrt {9{x^2}}  = 3x\)

B. \(\sqrt {9{x^2}}  =  - 3x\)

C. \(\sqrt {9{x^2}}  = 9x\)

D. \(\sqrt {9{x^2}}  =  - 9x\)

Câu 12. Tìm số tự nhiên n có hai chữ số, biết rằng tổng các chữ số của nó bằng 9 và nếu cộng thêm vào số đó 63 đơn vị thì được một số mới cũng viết bằng hai chữ số đó nhưng theo thứ tự ngược lại.

A. n = 36

B. n = 18

C. n = 45

D. n = 27

Câu 13. Cho \(Q = 4a - \sqrt {{a^2} - 4a + 4} ,\) với \(a \ge 2\) . Khẳng định nào sau đây đúng?

A. \(Q = 5a + 2.\)

B. \(Q = 3a - 2.\)

C. \(Q = 3a + 2.\)

D. \(Q = 5a - 2.\)

Câu 14. Biều thức \(M = {x^2} - 1\) bằng biểu thức nào sau đây?

A. \(M = \left( {1 - x} \right)\left( {x + 1} \right).\)

B. \(M = \left( {x - 1} \right)\left( {1 - x} \right).\)

C. \(M = \left( {x - 1} \right)\left( {x - 1} \right).\)

D. \(M = \left( {x - 1} \right)\left( {x + 1} \right).\)

Câu 15: Cho tam giác ABC, M thuộc cạnh AB, N thuộc cạnh BC, biết \(\dfrac{{MA}}{{MB}} = \dfrac{{NC}}{{NB}} = \dfrac{2}{5},MN = 15\left( {cm} \right).\). Tính độ dài cạnh AC.

A. AC = 21 (cm).                   

B. AC = 37,5 (cm)

C. AC = 52,5 (cm).                

D. AC = 25 (cm).

Câu 16. Cho hai đường tròn (O) và (O’) cắt nhau tại A, B. Tiếp tuyến tại A của đường tròn (O’) cắt (O) tại C và của (O) cắ (O’) tại D. Biết \(\widehat {ABC} = {75^0}\) . Tính \(\widehat {ABD}?\)

A. \(\widehat {ABD} = {40^0}.\)

B. \(\widehat {ABD} = {150^0}.\)

C. \(\widehat {ABD} = {50^0}.\)

D. \(\widehat {ABD} = {75^0}.\)

Câu 17. Số đo  3 góc của một tam giác tỉ lệ với các số 2; 3; 5. Tìm số đo của góc nhỏ nhất.

A. \({36^0}\)

B. \({18^0}\)

C. \({24^0}\)

D. \({54^0}\)

Câu 18. Trong các hình cho dưới đây, hình nào mô tả góc ở tâm?

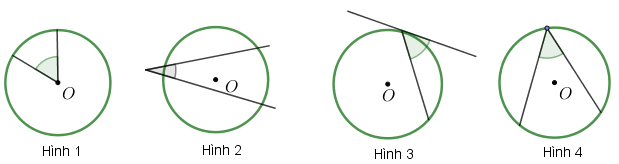
A. Hình 3 và Hình 4.

B. Hình 1.

C. Hình 2.

D. Hình 1 và Hình 4

Câu 19. Tính \(M = \dfrac{{\sqrt {12} }}{{\sqrt 3 }}\)

A. \(M = 4\)

B. \(M = 3\)

C. \(M = 1\)

D. \(M = 2\)

Câu 20. Cho \(P = \sqrt {4{a^2}}  - 6a.\) Khẳng định nào sau đây đúng?

A. \(P =  - 4a.\)

B. \(P =  - 4\left| a \right|.\)

C. \(P = 2a - 6\left| a \right|.\)

D. \(P = 2\left| a \right| - 6a.\)

Câu 21. Tính thể tích V của hình cầu có bán kính \(R = 3\left( {cm} \right).\)

A. \(V = 108\pi \left( {c{m^3}} \right)\)

B. \(V = 9\pi \left( {c{m^3}} \right)\)

C. \(V = 72\pi \left( {c{m^3}} \right)\)

D. \(V = 36\pi \left( {c{m^3}} \right)\)

Câu 22. Cho \(P = \sqrt {{{\left( {\sqrt 3  + 1} \right)}^2}}  + \sqrt {{{\left( {1 - \sqrt 3 } \right)}^2}} \) . Khẳng định nào sau đây đúng?

A. \(P = 2\)

B. \(P = 2 + 2\sqrt 3 \)

C. \(P = 2 - \sqrt 3 \)

D. \(2\sqrt 3 \)

Câu 23. Khẳng định nào sau đây sai?

A. \(\cos \,{35^0} > \sin {40^0}.\)

B. \(\sin {35^0} > \cos \,{40^0}.\)

C. \(\sin {35^0} < \sin \,{40^0}.\)

D. \(\cos \,{35^0} > \cos {40^0}.\)

Câu 24. Bạn An chơi thả diều. Tại thời điểm dây diều dài 80(m) và tạo với phương thẳng đứng một góc \({50^0}\) . Tính khoảng cách d từ diều đến mặt đất tại thời điểm đó (giả sử dây diều căng và không giãn; kết quả làm tròn đến chữ số thập phân thứ hai).

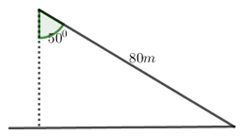
A. \(d \approx 51,42\left( m \right).\)

B. \(d \approx 57,14\left( m \right).\)

C. \(d \approx 54,36\left( m \right).\)

D. \(d \approx 61,28\left( m \right).\)

Câu 25. Tìm giá trị của m để hàm số \(y = \left( {2m - 1} \right)x + m + 2\)  cắt trục hoành tại điểm có hoành độ bằng \( - \dfrac{2}{3}\) .

A. \(m =  - \dfrac{1}{2}\)

B. \(m = \dfrac{1}{2}\)

C. \(m =  - 8\)

D. \(m = 8\)

Câu 26: Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có biệt thức \(\Delta  = {b^2} - 4ac < 0\). Khẳng định nào sau đây đúng?

A. Phương trình vô nghiệm.

B. Phương trình có nghiệm kép.

C. Phương trình có hai nghiệm phân biệt.

D. Phương trình có vô số nghiệm.

Câu 27. Tìm tất cả các giá trị của a, b để hệ phương trình \(\left\{ \begin{array}{l}2x + by =  - 4\\bx - ay =  - 5\end{array} \right.\)  có nghiệm (x;y) = (1;-2)

A. \(a = 2,b = 2\)

B. \(a =  - 4,b = 3\)

C. \(a =  - 3,b = 4\)

D. \(a =  - 4,b =  - 5\)

Câu 28. Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 1\\4x + y = 5\end{array} \right.\)

A. \(\left( {x;y} \right) = \left( { - 1; - 1} \right).\)

B. \(\left( {x;y} \right) = \left( { - 1;1} \right).\)

C. \(\left( {x;y} \right) = \left( {1;1} \right).\)

D. \(\left( {x;y} \right) = \left( {1; - 1} \right).\)

Câu 29. Tính bán kính r của đường tròn nội tiếp tam giác đều ABC cạnh a.

A. \(r = \dfrac{{a\sqrt 3 }}{6}.\)

B. \(r = a\sqrt 3 .\)

C. \(r = \dfrac{{a\sqrt 3 }}{3}.\)

D. \(r = \dfrac{{2a\sqrt 3 }}{3}.\)

Câu 30. Trong các số sau, số nào là số nguyên tố.

A. 29

B. 35.

C. 49.

D. 93

Câu 31. Cho một hình cầu có đường kính bằng 4 (cm). Tính diện tích S của hình cầu đó.

A. \(S = \dfrac{{16\pi }}{3}\left( {c{m^2}} \right)\) .

B. \(S = 16\pi \,\left( {c{m^2}} \right)\)

C. \(S = 64\pi \,\left( {c{m^2}} \right)\)

D. \(S = 32\pi \,\left( {c{m^2}} \right)\)

Câu 32. Trong các hàm số sau, hàm số nào đồng biến với mọi \(x \in R?\)

A. \(y =  - 2x + 4.\)

B. \(y = \sqrt 3 x - 2.\)

C. \(y =  - \left( {\dfrac{7}{2} + 2x} \right).\)

D. \(y = \dfrac{{1 - x}}{3}\)

Câu 33. Tìm điều kiện của m để hàm số \(y = \left( {2m - 1} \right)x + 2\)  luôn đồng biến.

A. \(m \ge \dfrac{1}{2}.\)

B. \(m < \dfrac{1}{2}.\)

C. \(m > \dfrac{1}{2}.\)

D. \(m \le \dfrac{1}{2}.\)

Câu 34. Cho tứ giác ABCD có \(AB = BC = CD = DA.\) Khẳng định nào sau đây đúng?

A. Tứ giác ABCD là hình vuông.

B. Tứ giác ABCD là hình chữ nhật.

C. Tứ giác ABCD là hình thoi.

D. Tứ giác ABCD là hình thang cân.

Câu 35. Rút gọn biểu thức \(M = {\left( {x - y} \right)^2} - {\left( {x + y} \right)^2}.\)

A. \(M =  - 2xy.\)

B. \(M =  - 4xy.\)

C. \(M =  - 2{x^2}.\)

D. \(M =  - 2{y^2}.\)

Câu 36. Tính chu vi của tam giác cân ABC. Biết AB = 6(cm); AC = 12(cm).

A. 25(cm)

B. 24(cm).

C. 30 (cm).

D. 15 (cm).

Câu 37. Giải phuong trình: \({x^2} - 5x + 6 = 0.\)

A. \({x_1} = 2;{x_2} = 3.\)

B. \({x_1} =  - 1;{x_2} =  - 6.\)

C. \({x_1} = 1;{x_2} = 6.\)

D. \({x_1} =  - 2;{x_2} =  - 3.\)

Câu 38. Cho \(P = 4 + {4^2} + ... + {4^{2018}} + {4^{2019}}.\) Tìm số dư khi chia P cho 20.

A. 8.

B. 16.

C. 4.

D. 12.

Câu 39. Cho tam giác ABC vuông tại A, đường cao AH và đường trung tuyến AM \(\left( {H,M \in BC} \right)\) . Biết chu vi của tam giác là 72cm và AM – AH = 7 (cm). Tính diện tích S của tam giác ABC.

A. \(S = 48\left( {c{m^2}} \right)\)

B. \(S = 108\left( {c{m^2}} \right)\)

C. \(S = 148\left( {c{m^2}} \right)\)

D. \(S = 144\left( {c{m^2}} \right)\)

Câu 40. Cho các số a, b, c thỏa mãn \({a^2} + {b^2} + {c^2} + 6 = 2\left( {a + 2b + c} \right).\) Tính tổng \(T = a + b + c.\)

A. \(T = 6.\)

B. \(T = 2.\)

C. \(T = 4.\)

D. \(T = 8.\)

Câu 41. Cho tam giác ABC có AB = 20(cm), BC = 12 (cm), CA = 16 (cm). Tính chu vi của đường tròn nội tiếp tam giác đã cho.

A. \(16\pi \left( {cm} \right).\)

B. \(20\pi \left( {cm} \right).\)

C. \(13\pi \left( {cm} \right).\)

D. \(8\pi \left( {cm} \right).\)

Câu 42: Biết các cạnh của một tứ giác tỉ lệ với 2; 3; 4; 5 và độ dài cạnh lớn nhất hơn độ dài cạnh nhỏ nhất là 6(cm). Tính chu vi của tứ giác đó.

A. 28 (cm).

B. 42 (cm).

C. 14 (cm)

D. 56 (cm).

Câu 43: Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - m + 3 = 0\) (m là tham số). Tìm các giá trị của m để phương trình đã cho có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10.\)

A. \(m = 1.\)

B. \(m = 4.\)

C. \(m =  - 1.\)

D. \(m =  - 4.\)

Câu 44. Cho tam giác ABC, biết \(\widehat B = {60^0},AB = 6\left( {cm} \right),BC = 4\left( {cm} \right).\) Tính độ dài của cạnh AC.

A. \(AC = 2\sqrt 7 \left( {cm} \right).\)

B. \(AC = \sqrt {52} \left( {cm} \right).\)   

C. \(AC = 4\sqrt 5 \left( {cm} \right).\)     

D. \(AC = 2\sqrt 3 \left( {cm} \right).\)

Câu 45. Mặt cầu (S) được gọi là ngoại tiếp hình lập phương ABCD.A’B’C’D’ nếu các đỉnh của hình laapoj phương đều thuộc mặt cầu (S). Biết hình lập phương có độ dài cạnh 2a, tính thể tích V của hình cầu ngoại tiếp hình lập phương đó.

A. \(V = 3\pi {a^3}.\)   

B. \(V = 4\sqrt 3 \pi {a^3}.\)   

C. \(V = \dfrac{{\sqrt 3 }}{2}\pi {a^3}.\)   

D. \(V = 3\sqrt 2 \pi {a^3}.\)

Câu 46. Cho \(\widehat {xOy} = {45^0}.\) Trên tia Oy lấy hai điểm A, B sao cho \(AB = \sqrt 2 \left( {cm} \right).\) Tính độ dài hình chiếu vuông góc của đoạn thẳng AB trên Ox.

A. \(\dfrac{{\sqrt 2 }}{2}\left( {cm} \right).\)

B. \(\dfrac{{\sqrt 2 }}{4}\left( {cm} \right).\)

C. \(1\left( {cm} \right).\)

D. \(\dfrac{1}{2}\left( {cm} \right).\)

Câu 47: Một tấm tôn hình chữ nhật có chu vi là 48 cm. Người ta cắt bỏ mỗi góc của tấm tôn một hình vuông có cạnh 2cm rồi gấp lên thành một hình hộp chữ nhật không nắp có thể tích \(96c{m^3}.\) Giả sử tấm tôn có chiều dài là a, chiều rộng là b. Tính giá trị biểu thức \(P = {a^2} - {b^2}.\)

A. P = 80                                 B. P = 112.     

C. P = 192.                              D. P = 256.

Câu 48.  Hai vòi nước cùng chảy vào một bể không có nước. Nếu cho vòi một chảy trong 3 giờ rồi hóa lại, sau đó cho vòi hai chảy tiếp trong 8 giờ nữa thì đầy bể. Nếu cho vòi một chảy trong 1 giờ, rồi cho cả hai vòi chảy tiếp trong 4 giờ nữa thì số nước chảy vào bằng \(\dfrac{8}{9}\)  bể. Hỏi nếu chảy một mình thì vòi một sẽ chảy trong thời gian t bằng bao nhiêu thì đầy bể?

A. t  = 10 giờ.                         B. t = 12 giờ.       

C. t = 11 giờ.                          D. t = 9 giờ.

Câu 49. Kết quả rút gọn biểu thức \(A = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x  - 2}} + \dfrac{1}{{\sqrt x  + 2}}\) với \(x \ge 0,x \ne 4\)  có dạng \(\dfrac{{\sqrt x  - m}}{{\sqrt x  + n}}.\) Tính giá trị của m – n.          

A. \(m - n =  - 2.\)       

B. \(m - n =  - 4.\)         

C. \(m - n = 4.\)           

D. \(m - n = 2.\)

Câu 50. Cho hình vuông ABCD cạnh bằng a. Gọi E là trung điểm của CD. Tính độ dài dây cung chung CF của đường tròn đường kính BE và đường tròn đường kính CD.

A. \(CF = a.\)     

B. \(CF = \dfrac{{2a\sqrt 5 }}{5}.\)     

C. \(CF = \dfrac{{2a\sqrt 3 }}{3}.\)   

D. \(CF = \dfrac{{a\sqrt 5 }}{5}.\)

Câu I 

1. Tính giá trị của biểu thức \(A = \sqrt 5 \left( {\sqrt {20}  - \sqrt 5 } \right) + 1\)

2. Tìm tham số m để đường thẳng \(y = \left( {m - 1} \right)x + 2018\) có hệ số góc bằng 3.

Câu II 

1. Giải hệ phương trình \(\left\{ \begin{array}{l}x + 4y = 8\\2x + 5y = 13\end{array} \right.\)

2. Cho biểu thức \(B = \left( {\dfrac{6}{{a - 1}} + \dfrac{{10 - 2\sqrt a }}{{a\sqrt a  - a - \sqrt a  + 1}}} \right).\dfrac{{{{\left( {\sqrt a  - 1} \right)}^2}}}{{4\sqrt a }}\) (với \(a > 0,\,a \ne 1\))

a) Rút gọn biểu thức B.

b) Đặt \(C = B.\left( {a - \sqrt a  + 1} \right)\). So sánh C và 1.

3. Cho phương trình \({x^2} - \left( {m + 2} \right)x + 3m - 3 = 0\,\,\left( 1 \right)\), với x là ẩn, m là tham số.

a)  Giải phương trình (1) khi \(m =  - 1.\)

b)  Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1};\,\,{x_2}\) sao cho  \({x_1};\,\,{x_2}\) là độ dài hai cạnh góc vuông của một tam giác vuông có độ dài cạnh huyền bằng 5.

Câu III 

Bạn Linh đi xe đạp từ nhà đến trường với quãng đường 10 km. Khi đi từ trường về nhà, vẫn trên cung đường ấy, do lượng xe tham gia giao thông nhiều hơn nên bạn Linh phải giảm vận tốc 2 km/h so với khi đến trường. Vì vậy thời gian về nhà nhiều hơn thời gian đến trường là 15 phút. Tính vận tốc của xe đạp khi bạn Linh đi từ nhà đến trường.

Câu IV 

Cho tam giác \(ABC\) nhọn. Đường tròn tâm O đường kính BC cắt các cạnh \(AB,AC\) lần lượt tại các điểm \(M,N\,\,\left( {M \ne B,N \ne C} \right)\). Gọi H là giao điểm của BN và CM; P là giao điểm của AH và BC.

1. Chứng minh tứ giác AMHN nội tiếp được trong một đường tròn.

2. Chứng minh \(BM.BA = BP.BC\).

3. Trong trường hợp đặc biệt khi tam giác \(ABC\) đều cạnh bằng \(2a\) . Tính chu vi đường tròn ngoại tiếp tứ giác AMHN.

4. Từ điểm A kẻ các tiếp tuyến AE và AF của đường tròn tâm O đường kính BC (E, F là các tiếp điểm). Chứng minh ba điểm \(E,H,F\) thẳng hàng.

Câu V 

Tìm giá trị nhỏ nhất của biểu thức \(\) với \(x > 0\)

Bài 1 

Cho biểu thức: \(A = \left( {\dfrac{1}{{x + \sqrt x }} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x }}{{x + 2\sqrt x  + 1}},\) với \(x > 0.\)

a) Rút gọn biểu thức: \(A.\)

b) Tìm các giá trị của \(x\) để \(A > \dfrac{1}{2}.\)

Bài 2 

1) Không dùng máy tính, trình bày cách giải hệ phương trình: \(\left\{ \begin{array}{l}2x - y = 4\\x + 3y =  - 5\end{array} \right..\)

2) Trong mặt phẳng tọa độ \(Oxy\) đường thẳng \(d\) có hệ số góc \(k\) đi qua điểm \(M\left( {1; - 3} \right)\) cắt các trục \(Ox,\;\;Oy\) lần lượt tại \(A\) và \(B.\)

a) Xác định tọa độ các điểm \(A,\;\;B\) theo \(k.\)

b) Tính diện tích tam giác \(OAB\) khi \(k = 2.\)

Bài 3

 Tìm một số có hai chữ số biết rằng: Hiệu của số ban đầu với số đảo ngược của nó bằng  18 (số đảo ngược của một số là số thu được bằng cách viết các chữ số của số đó theo thứ tự ngược lại) và tổng của số ban đầu với bình phương số đảo ngược của nó bằng 618.

Bài 4 

Cho tam giác đều ABC có đường cao AH. Trên cạnh BC lấy điểm M tùy ý (M không trùng với B, C, H). Gọi P, Q lần lượt là hình chiếu vuông góc vủa M lên AB và AC.

a)  Chứng minh tứ giác APMQ nội tiếp được trong đường tròn và xác định tâm O của đường tròn này.

b)  Chứng minh \(OH \bot PQ\).

c)  Chứng minh \(MP + MQ = AH\).

Bài 5 

Cho tam giác đều \(ABC\) có cạnh bằng \(a.\) Hai điểm \(M,\;N\) lần lượt di động trên hai đoạn thẳng \(AB,\;\;AC\) sao cho \(\dfrac{{AM}}{{MB}} + \dfrac{{AN}}{{NC}} = 1.\) Đặt \(AM = x\) và \(AN = y.\) Chứng minh: \(MN = a - x - y.\)

Câu 1 

 Giải phương trình và hệ phương trình sau:

a) \(2{x^2} - 3x - 2 = 0\)

b) \(\left\{ \begin{array}{l}2x - 3y = 12\\3x + y = 7\end{array} \right.\)

Câu 2 

a) Rút gọn biểu thức \(A = \sqrt {9 - 4\sqrt 5 }  + \dfrac{1}{{\sqrt 5  - 2}}\)

b) Vẽ đồ thị của hàm số \(y = \dfrac{3}{4}{x^2}.\)

Câu 3 

a) Khi thực hiện xây dựng trường điển hình đổi mới năm 2017, hai trường trung học cơ sở A và B có tất cả 760 học sinh đăng ký tham gia nội dung hoạt động trải nghiệm. Đến khi tổng kết, số học sinh tham gia đạt tỷ lệ 85% so với số đã đăng ký. Nếu tính riêng thì tỷ lệ học sinh tham gia của trường A và trường B lần lượt là 80% và 89,5%. Tính số học sinh ban đầu đăng ký tham gia của mỗi trường.

b) Tìm tất cả các giá trị của tham số \(m\) sao cho phương trình \(2{x^2} - \left( {m + 5} \right)x - 3{m^2} + 10m - 3 = 0\) có hai nghiệm phân biệt \({x_1},\;\;{x_2}\) thỏa mãn \(x_1^2 + x_2^2 - \left( {{x_1} + {x_2}} \right) + {x_1}{x_2} = 4.\)

Câu 4 

Cho đường tròn tâm O và điểm P nằm ngoài (O). Vẽ tiếp tuyến PC của (O) (C là tiếp điểm) và cát tuyến PAB (PA < PB) sao cho các điểm A, B, C nằm cùng phía so với đường thẳng PO. Gọi M là trung điểm của đoạn AB và CD là đường kính của (O).

a) Chứng minh tứ giác PCMO là tứ giác nội tiếp.

b) Gọi E là giao điểm của đường thẳng PO với đường thẳng BD. Chứng minh AM.DE = AC.DO.

c) Chứng minh đường thẳng CE vuông góc với đường thẳng CA.

Câu 1. 

1)  Tìm \(x\) , biết \(2\sqrt x  = 3.\)

2) Giải phương trình: \(43{x^2} - 2018x + 1975 = 0.\)

3)      Cho hàm số \(y = \left( {a + 1} \right){x^2}.\) Tìm a để hàm số nghịch biến khi \(x < 0\)  và đồng biến khi \(x > 0.\)

Câu 2. Cho phương trình: \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 2 = 0\,\,\left( 1 \right),\) m là tham số

1) Tìm m để \(x = 2\) là nghiệm của phương trình (1).

2)  Xác định m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn điều kiện: \(x_1^2 + x_2^2 = 10\)

Câu 3. 

1) Trong mặt phẳng tọa độ \(Oxy\) cho các đường thẳng có phương trình: \(\left( {{d_1}} \right):\;\;y = x + 2,\;\;\left( {{d_2}} \right):\;\;y =  - 2\)  và \(\;\left( {{d_3}} \right):\;\;y = \left( {k + 1} \right)x + k.\) Tìm \(k\) để các đường thẳng trên đồng quy.

2) Rút gọn và tìm giá trị lớn nhất của biểu thức:\(A = \left( {\dfrac{1}{{1 - \sqrt x }} + \dfrac{{x + 2}}{{x\sqrt x  - 1}} + \dfrac{{\sqrt x }}{{x + \sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{3}\) (với \(x \ge 0,x \ne 1\)).

Câu 4. 

Cho tam giác \(ABC\) có ba góc nhọn và \(\widehat {A\;} = {45^0}.\)  Gọi \(D,\;E\)  lần lượt là hình chiếu vuông góc của \(B,\;C\) lên \(AC,\;AB;\;H\) là giao điểm của \(BD\) và \(CE.\)

1) Chứng minh tứ giác \(BEDC\) nội tiếp.

2) Chứng minh \(DE.AB = BC.AD\) và tính tỉ số \(\dfrac{{ED}}{{BC}}.\)

3) Chứng minh \(HE + HD = BE + CD.\)

4) Gọi \(I\) là tâm đường tròn ngoại tiếp tam giác \(ABC.\) Chứng minh \(AI \bot DE.\)

Câu 5.

Cho \(n\) là số tự nhiên khác \(0.\) Tìm giá trị nhỏ nhất của:

 \(Q = \sqrt {1 + \dfrac{1}{{{1^2}}} + \dfrac{1}{{{2^2}}}}  + \sqrt {1 + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}}}  \)\(\,+ \sqrt {1 + \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}}}  + .....\)\(\, + \sqrt {1 + \dfrac{1}{{{n^2}}} + \dfrac{1}{{{{\left( {n + 1} \right)}^2}}}}  + \dfrac{{101}}{{n + 1}}.\)

Câu 1

a) Tính \(H = \sqrt {81}  - \sqrt {16} .\)

b) Tìm điều kiện của \(x\) để \(\sqrt {x + 2} \) có nghĩa.

Câu 2 

Giải hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 3\\3x + 2y = 1\end{array} \right..\)

Câu 3 

Rút gọn biểu thức \(M = \left( {\dfrac{{x + \sqrt y  + \sqrt {xy}  - 1}}{{\sqrt x  + 1}} + 1} \right).\left( {\sqrt x  - \sqrt y } \right)\) (với \(x \ge 0,\;y \ge 0\)).

Câu 4 

a) Giải phương trình \({x^2} - 2x - 8 = 0.\)

b) Cho phương trình \({x^2} + 6x + m = 0\) (với m là tham số). Tìm tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt.

Câu 5 

Trong mặt phẳng tọa độ \(Oxy,\) cho đường thẳng  \(\left( d \right):\;y =  - 3x + b\) và parabol \(\left( P \right):\;\;y = 2{x^2}.\)

a) Xác định hệ số b để (d) đi qua điểm \(A\left( {0;\;1} \right).\)

b) Với \(b =  - 1,\) tìm tọa độ giao điểm của (d) và (P) bằng phương pháp đại số.

Câu 6 

Để chuẩn bị cho mùa giải sắp tới, một vận động viên đua xe ở Đồng Tháp đã luyện tập leo dốc và đổ dốc trên cầu Cao Lãnh. Biết rằng đoạn leo dốc và đổ dốc ở hai bên đầu cầu có độ dài cùng bằng \(1km.\) Trong một lần luyện tập, vận động viên khi đổ dốc nhanh hơn vận tốc khi leo dốc là \(9km/h\) và tổng thời gian hoàn thành là \(3\) phút. Tính vận tốc leo dốc của vận động viên trong lần luyện tập đó.

Câu 7. Nhằm tiếp tục đẩy mạnh phong trào xây dựng trường học Xanh – Sạch – Đẹp, trường THCS A đã thiết kế một khuôn viên để trồng hoa có dạng hình tam giác vuông (như hình bên, biết rằng \(\Delta MNK\) vuông tại M, \(MN = 6m,\,\,MK = 8m,\,\,MH \bot NK\)). Nhà trường trồng hoa mười giờ dọc các đoạn NK, MH.

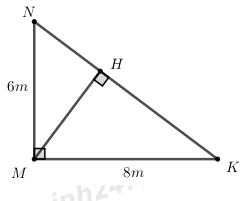
a)  Tính độ dài các đoạn NK, MH.

b)  Biết rằng chi phí trồng hoa mười giờ là 20000 đồng trên mỗi mét chiều dài. Tính tổng chi phí để trồng các luống hoa mười giờ đó.

Câu 8. Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right)\), đường cao \(AH\,\,\left( {H \in BC} \right)\), trên cạnh BC lấy điểm D sao cho \(BD = BA\), vẽ CE vuông góc AD \(\left( {E \in AD} \right)\).

a)  Chứng minh tứ giác AHEC là tứ giác nội tiếp.

b)  Chứng minh \(DA.HE = DH.AC\)

c)  Chứng minh tam giác \(EHC\) là tam giác cân.

Câu 1 

Giải phương trình và hệ phương trình:

\(1)\;\;\dfrac{{3x + 1}}{2} - x = 1\)   

\(2)\;\;\left\{ \begin{array}{l}3x = 17 - y\\x - 2y = 1\end{array} \right.\)

Câu 2 

1) Tìm \(m\) để phương trình \({d_1}:\;y = \left( {{m^2} + 1} \right)x + 2m - 3\) cắt đường thẳng \(d:\;y = x - 3\) tại điểm \(A\) có hoành độ bằng \( - 1.\)

2) Rút gọn biểu thức \(A = \left( {\dfrac{1}{{x + \sqrt x }} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{{x + 2\sqrt x  + 1}} + 1\) với \(x > 0,\;\;x \ne 1.\)

Câu 3 (2 điểm):

1) Quãng đường Hải Dương – Hạ Long dài 100km. Một ô tô đi từ Hải Dương đến Hạ Long rồi nghỉ ở đó 8 giờ 20 phút, sau đó trở về Hải Dương hết tất cả 12 giờ. Tính vận tốc của ô tô lúc đi, biết vận tốc ô tô lúc về nhanh hơn vận  tốc ô tô lúc đi 10 km/h.

2) Tìm \(m\) để phương trình \({x^2} - 2mx + {m^2} - 2 = 0\) (x là ẩn, m là tham số) có hai nghiệm phân biệt \({x_1},\;{x_2}\) thỏa mãn \(\left| {x_1^3 - x_2^3} \right| = 10\sqrt 2 .\)

Câu 4

Cho tam giác ABC nội tiếp đường tròn tâm O đường kính BC. Kẻ AH vuông góc với BC (H thuộc BC), gọi M, N lần lượt là hình chiếu vuông góc của H trên AB và AC.

1) Chứng minh \(A{C^2} = CH.CB.\)

2) Chứng minh tứ giác \(BCNM\) nội tiếp và \(AC.BM + AB.CN = AH.BC.\)

3) Đường thẳng đi qua A cắt tia HM tại E và cắt tia đối của tia NH tại F. Chứng minh BE // CF.

Câu 5 

Cho phương trình \(a{x^2} + bx + c = 0\;\;\left( {a \ne 0} \right)\) có hai nghiệm \({x_1},\;{x_2}\) thỏa mãn \(0 \le {x_1} \le {x_2} \le 2.\) Tìm giá trị nhỏ nhất của biểu thức \(L = \dfrac{{3{a^2} - ab + ac}}{{5{a^2} - 3ab + {b^2}}}.\)

Câu 1 

a) Tính \(E = 2\sqrt {48}  + 3\sqrt {75}  - 2\sqrt {108} .\)

b) Tìm điều kiện xác định và rút gọn biểu thức \(P\left( x \right) = \left( {\dfrac{1}{{{x^2} - x}} + \dfrac{1}{{x - 1}}} \right):\dfrac{{x + 1}}{{{x^2} - 2x + 1}}.\)

Câu 2 

a) Vẽ đồ thị \(\left( P \right)\) của hàm số \(y = 2{x^2}\) trên hệ trục tọa độ \(Oxy.\)

b) Tìm các giá trị của tham số \(m\) để đường thẳng \(\left( {{d_m}} \right):\;\;y = \left( {{m^2} + m - 4} \right)x + m - 7\) song song với đường thẳng \(\left( d \right):\;\;y = 2x - 5.\)

Câu 3 

a) Gọi \({x_1},\;{x_2}\) là hai nghiệm của phương trình \({x^2} - 2\left( {m - 1} \right)x - 2m - 7 = 0\)  (\(m\) là tham số). Tìm các giá trị của \(m\) để biểu thức \(A = x_1^2 + x_2^2 + 6{x_1}{x_2}\) đạt giá trị nhỏ nhất.

b) Bạn Nam mua hai món hàng và phải trả tổng cộng 480000 đồng, trong đó đã tính cả 40000 đồng là thuế giá trị gia tăng (viết tắt là thuế VAT). Biết rằng thuế VAT đối với mặt hàng thứ nhất là 10%, thuế VAT đối với mặt hàng thứ hai là 8%. Hỏi nếu không kể thuế VAT thì bạn Nam phải trả mỗi món hàng là bao nhiêu tiền?

(Trong đó: Thuế VAT là thuế mà người mua hàng phải trả, người bán hàng thu và nộp cho Nhà nước. Giả sử thuế VAT đối với mặt hàng A được quy là 10%. Khi đó nếu giá bán của mặt hàng A là x đồng thì kể cả thuế VAT, người mua phải trả tổng cộng là \(x + 10\% x\) đồng).

Câu 4 (0,5 điểm):

Cho biểu thức \(Q\left( x \right) = \dfrac{{5{x^2} + 6x + 2018}}{{x + 1}}.\) Tìm các giá trị nguyên của \(x\) để \(Q\left( x \right)\) là số nguyên.

Câu 5 

Cho đường tròn \(\left( O \right),\) từ điểm \(A\) ngoài đường tròn vẽ đường thẳng \(AO\) cắt đường tròn \(\left( O \right)\) tại \(B,\;\;C\;\left( {AB < AC} \right).\) Qua \(A\) vẽ đường thẳng không đi qua \(O\) cắt đường tròn \(\left( O \right)\) tại \(D,\;E\;\;\left( {AD < AE} \right).\) Đường thẳng vuông góc với \(AB\) tại \(A\) cắt đường thẳng \(CE\) tại \(F.\)

a) Chứng minh tứ giác \(ABEF\) nội tiếp.

b) Gọi \(M\) là giao điểm thứ hai của \(FB\) với đường tròn \(\left( O \right).\) Chứng minh \(DM \bot AC.\)

c) Chứng minh \(CE.CF + AD.AE = A{C^2}.\)

Câu 1

Thực hiện phép tính: \(\left( {\sqrt 3  + 1} \right).\dfrac{{\sqrt 3  - 3}}{{2\sqrt 3 }}.\)

Câu 2 

Cho hàm số \(y =  - \dfrac{1}{2}{x^2}\) có đồ thị \(\left( P \right)\) và đường thẳng \(\left( d \right):\;\;y = 3 - 4x.\) Lập phương trình đường thẳng \(\left( \Delta  \right)\) song song với \(\left( d \right)\) và cắt \(\left( P \right)\) tại điểm \(M\) có hoành độ bằng \(2.\)

Câu 3

Rút gọn biểu thức sau: \(A = \left( {1 - \dfrac{{2\sqrt x }}{{3\sqrt x  + 1}} - \dfrac{{1 - 2\sqrt x }}{{1 - 9x}}} \right):\left( {\dfrac{{6\sqrt x  + 5}}{{3\sqrt x  + 1}} - 2} \right)\)\(\;\;\;\left( {x \ge 0,\;\;x \ne \dfrac{1}{9}} \right).\)

Câu 4 

Cho phương trình \({x^2} - x + m + 1 = 0\)  (m là tham số).

a) Giải phương trình với \(m =  - 3.\)

b) Tìm tất cả các giá trị của m để phương trình đã cho có hai nghiệm \({x_1},\;{x_2}\) thỏa mãn điều kiện: \(\left| {{x_1} - {x_2}} \right| = 2.\)

Câu 5 

Một tam giác vuông có chu vi bằng 24 cm. Độ dài hai cạnh góc vuông hơn kém nhau 2 cm. Tính diện tích tam giác vuông đó.

Câu 6  Cho hình nón có bán kính đáy bằng 3m, diện tích toàn phần bằng \(24\pi \,\,{m^2}\). Tính thể tích của hình nón.

Câu 7  Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao AA’, BB’, CC’ của tam giác ABC cắt nhau tại H. Đường thẳng AO cắt đường tròn tâm O tại D khác A.

a) Chứng minh tứ giác AB’HC’ nội tiếp đường tròn.

b)  Gọi I là giao điểm của hai đường thẳng HD và BC. Chứng minh I là trung điểm của đoạn BC.

c) Tính \(\dfrac{{AH}}{{AA'}} + \dfrac{{BH}}{{BB'}} + \dfrac{{CH}}{{CC'}}\).

Câu 8 Tìm giá trị nhỏ nhất của biểu thức \(T = 3{x^2} + 4{y^2} + 4xy + 2x - 4y + 2021\)

Câu 1 

a) So sánh \(2\sqrt 3  + \sqrt {27} \) và \(\sqrt {74} .\)

b) Chứng minh đẳng thức: \(\left( {\dfrac{1}{{\sqrt x  - 2}} - \dfrac{1}{{\sqrt x  + 2}}} \right).\dfrac{{x - 4}}{4} = 1,\) với \(x \ge 0\) và \(x \ne 4.\)

c) Tìm giá trị của \(m\) để đồ thị hàm số \(y = 3x + m\) đi qua điểm \(A\left( {1;\;2} \right).\)

Câu 2 

Cho phương trình \({x^2} + 2x + m - 1 = 0\;\;\;\;\left( * \right),\) trong đó \(m\) là tham số.

a) Giải phương trình \(\left( * \right)\) khi \(m =  - 2.\)

b) Tìm \(m\) để phương trình \(\left( * \right)\) có hai nghiệm phân biệt \({x_1}\) và \({x_2}\) thỏa mãn điều kiện \({x_1} = 2{x_2}.\)

Câu 3 

Nhân ngày sách Việt Nam, 120 học sinh khối 8 và 100 học sinh khối 9 cùng tham gia phong trào xây dựng “Tủ sách nhân ái”. Sau một thời gian phát động, tổng số sách cả hai khối đã quyên góp được là 540 quyển. Biết rằng mỗi học sinh khối 9 quyên góp nhiều hơn nhiều hơn mỗi học sinh khối 8 một quyển. Hỏi mỗi khối đã quyên góp được bao nhiêu quyển sách? (Mỗi học sinh trong cùng một khối quyên góp số lượng sách như nhau).

Câu 4 

Cho đường tròn (O) có dây BC  cố định không đi qua tâm O. Điểm A di động trên (O) sao cho tam giác ABC có 3 góc nhọn. Các đường cao BE, CF của tam giác ABC (E thuộc AC, F thuộc AB) cắt nhau tại H. Gọi K là giao điểm của hai đường thẳng EF và BC, đoạn thẳng KA cắt (O) tại điểm M. Chứng minh rằng:

a) BCEF là tứ giác nội tiếp.

b) KM.KA = KE.KF.

c) Đường thẳng MH luôn đi qua một điểm cố định khi A thay đổi.

Câu 5 

Giải hệ phương trình: \(\left\{ \begin{array}{l}x\left( {2x - 2y + 1} \right) = y\\y + 2\sqrt {1 - x - 2{x^2}}  = 2\left( {1 + {y^2}} \right)\end{array} \right..\)

PHẦN I – TRẮC NGHIỆM (2,0 điểm)

Câu 1. Điều kiện để biểu thức \(\sqrt {4 - 2x} \) xác định là:

A. \(x \le 2\)

B. \(x > 2\)

C. \(x \ne 2.\)

D. \(x \ge 2\)

Câu 2. Trên mặt phẳng tọa độ Oxy, đồ thị hàm số \(y =  - 2x + 4\) cắt trục hoành tại điểm

A. \(M\left( {0;2} \right).\)

B. \(N\left( {2;0} \right).\)

C. \(P\left( {4;0} \right)\)

D. \(Q\left( {0;4} \right).\)

Câu 3. Phương trình nào sau đây có hai nghiệm phân biệt và tích hai nghiệm là một số dương?

A. \({x^2} - x + 1 = 0.\)

B. \( - 4{x^2} + 4x - 1 = 0.\)

C. \({x^2} - 3x + 2 = 0.\)

D. \(2{x^2} - 5x - 1 = 0.\)

Câu 4. Trong các hàm số sau, hàm số nào đồng biến khi \(x < 0\) ?

A. \(y =  - 2x.\)

B. \(y = 3 + \left( {2 - \sqrt 5 } \right)x.\)

C. \(y = \sqrt 3 {x^2}.\)

D. \(y = \left( {\sqrt 3  - 2} \right){x^2}.\)

Câu 5. Tất cả các giá trị của m để hai đường thẳng \(y = 2x + m + 2\)  và \(y = \left( {{m^2} + 1} \right)x + 1\) song song với nhau là

A. \(m = 1.\)

B. \(m =  - 1.\)

C. \(m =  \pm 1.\)

D. \(m \in \emptyset \)  

Câu 6. Nếu tăng bán kính của một hình tròn lên gấp 3 lần thì diện tích của hình tròn đó tăng lên gấp

A. 3 lần.

B. 6 lần.

C. 9 lần.

D. 27 lần.

Câu 7. Một tam giác có độ dài ba cạnh lần lượt là 5 cm, 12 cm, 13 cm, bán kính đường tròn ngoại tiếp tam giác đó là:

A. \(\dfrac{5}{2}cm.\)

B. \(5\,cm.\)

C. \(\dfrac{{13}}{2}\,cm.\)

D. \(13\,cm.\)

Câu 8. Hình trụ có bán kính đáy bằng 9cm, diện tích xung quanh bằng \(198\pi \,\,c{m^2}\) , chiều cao hình trụ đó bằng

A. 9 cm.

B. 11 cm.

C. 12 cm.

D. 22 cm.

PHẦN II – TỰ LUẬN (8,0 điểm)

Câu 1. (1,5 điểm) Cho biểu thức \(M = \left( {\dfrac{{4x}}{{\sqrt x  - 1}} - \dfrac{{\sqrt x  - 2}}{{x - 3\sqrt x  + 2}}} \right).\dfrac{{\sqrt x  - 1}}{{{x^2}}}\)  (với \(x > 0;x \ne 1;x \ne 4\))

1) Rút gọn biểu thức M.

2) Tìm các giá trị x để M < 4

Câu 2 (1,5 điểm): Cho phương trình \({x^2} - mx - 4 = 0\;\;\;\left( 1 \right)\)  (với m là tham số)

a) Giải phương trình \(\left( 1 \right)\) với \(m = 3.\)

b) Chứng minh rằng với mọi giá trị \(m\) thì phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt \({x_1},\;\;{x_2}.\) Tìm \(m\) để \(x_1^2 + x_2^2 = 17?\) 

Câu 3. (1,0 điểm). Giải hệ phương trình: \(\left\{ \begin{array}{l}\sqrt {xy}  - \dfrac{4}{{\sqrt {xy} }} = 3\\x\left( {1 - y} \right) + 15 = 0\end{array} \right.\)

Câu 4. Cho đường tròn \(\left( O \right)\) đường kính AB và điểm C trên đường tròn \(\left( {C \ne A;C \ne B} \right)\). Gọi D là một điểm trên cung nhỏ \(CB\,\,\left( {D \ne C;D \ne B} \right)\) ; E là giao điểm của AD và BC; I là hình chiếu vuông góc của E trên AB; M là điểm thứ hai của đường thẳng DI và đường tròn \(\left( O \right)\).

1)  Chứng minh tứ giác BDEI là tứ giác nội tiếp và \(CM \bot AB\).

2)  Gọi K là giao điểm của BC và DM. Chứng minh \(BK.CE = BC.EK\)

Câu 5.

1)  Hai đại biểu của trường A và trường B tham dự một buổi hội thảo. Mỗi đại biểu của trường A lân lượt bắt tay với từng đại biểu của trường B một lần. Tính số đại biểu của mỗi trường, biết số cái bắt tay bằng ba lần tổng số đại biểu của cả hai trường và số đại biểu của trường A nhiều hơn số đại biểu của trường B.

2) Cho \(x,y,z\) là các số dương. Chứng minh rằng \(\dfrac{{2\sqrt x }}{{{x^3} + {y^2}}} + \dfrac{{2\sqrt y }}{{{y^3} + {z^2}}} + \dfrac{{2\sqrt z }}{{{z^3} + {x^2}}} \le \dfrac{1}{{{x^2}}} + \dfrac{1}{{{y^2}}} + \dfrac{1}{{{z^2}}}\)

I. TRẮC NGHIỆM 

Câu 1: Tìm tất cả các giá trị của \(x\) để biểu thức \(\sqrt {x - 2} \) có nghĩa.

A. \(x \ge 2\)                            B. \(x > 2\)      

C. \(x \le 2\)                             D. \(x \ge 0\)

Câu 2:   Hàm số nào dưới đây là hàm số bậc nhất?

A. \(y = \sqrt {x + 2} \)                      

B. \(y = \dfrac{2}{x} + 1\)               

C. \(y =  - 2x + 1\)          

D. \(y = {x^2}\)

Câu 3:  Tìm \(m\) biết điểm \(A\left( {1;\; - 2} \right)\) thuộc đường thẳng có phương trình \(y = \left( {2m - 1} \right)x + 3 + m.\)

A. \(m =  - \dfrac{4}{3}\)        

B. \(m = \dfrac{4}{3}\)         

C. \(m = \dfrac{5}{3}\)       

D. \(m =  - \dfrac{5}{3}\)  

Câu 4:  Tìm tất cả các giá trị của \(m\) để hàm số \(y = \left( {2m - 1} \right)x + m + 2\) đồng biến trên \(R.\) 

A. \(m < \dfrac{1}{2}\)               

B. \(m > \dfrac{1}{2}\)           

C. \(m > 0\)           

D. \(m < 0\)  

Câu 5: Hàm số nào dưới đây đồng biến khi \(x < 0\) và nghịch biến khi \(x > 0?\)  

A. \(y =  - 3x + 1\)     

B. \(y = x - 3\)                 

C. \(y = {x^2}\)           

D. \(y =  - 3{x^2}\)

Câu 6: Tìm tất cả các giá trị của \(m\) để phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 3 = 0\) vô nghiệm.

A. \(m \ge  - 2\)             

C. \(m >  - 2\)      

D. \(m <  - 2\)  

Câu 7: Phương trình nào dưới đây có tổng hai nghiệm bằng 3?

A. \(2{x^2} + 6x + 1 = 0\)        

B. \(2{x^2} - 6x + 1 = 0\)     

C. \({x^2} - 3x + 4 = 0\)     

D. \({x^2} + 3x - 2 = 0\)

Câu 8:  Cho tam giác ABC  vuông tại A. Khẳng định nào dưới đây đúng?  

A. \(\cos B = \dfrac{{AB}}{{BC}}\)

B. \(\cos B = \dfrac{{AC}}{{BC}}\)      

C. \(\cos B = \dfrac{{AB}}{{AC}}\)           

D. \(\cos B = \dfrac{{AC}}{{AB}}.\) 

Câu 9:  Khẳng định nào dưới đây sai?

A. Mọi hình vuông đều là tứ giác nội tiếp.             

B. Mọi hình chữ nhật đều là tứ giác nội tiếp.

C. Mọi hình thoi đều là tứ giác nội tiếp.                   

D. Mọi hình thang cân đều là tứ giác nội tiếp.

Câu 10:  Cho đường tròn tâm \(O,\) bán kính \(R = 5\;cm\) có dây cung \(AB = 6\;cm.\) Tính khoảng cách  \(d\) từ \(O\) tới đường thẳng \(AB.\)   

A. \(d = 1\;cm.\)                      

B. \(d = 2\;cm.\)             

D. \(d = \sqrt {34} \;cm.\)

II. TỰ LUẬN: 

Câu 1 

Hai bạn Hòa và Bình có 100 quyển sách. Nếu Hòa cho Bình 10 quyển sách thì số quyển sách của Hòa bằng \(\dfrac{3}{2}\) số quyển sách của Bình. Hỏi lúc đầu mỗi bạn có bao nhiêu quyển sách?

Câu 2 

Trên mặt phẳng tọa độ \(Oxy\) cho đường thẳng \(\left( d \right)\) đi qua \(A\left( {3;\;7} \right)\) và song song với đường thẳng có phương trình \(y = 3x + 1.\)

a) Viết phương trình đường thẳng \(\left( d \right).\)

b) Tìm tọa độ giao điểm của đường thẳng \(\left( d \right)\) và parabol \(\left( P \right):\;\;y = {x^2}.\)

Câu 3 

Cho đường tròn (O; R) và điểm M cố định nằm ngoài (O; R). Từ M  kẻ các tiếp tuyến MA, MB tới (O; R) (A, B là các tiếp điểm). Đường thẳng (d) bất kỳ qua M và cắt (O; R) tại hai điểm phân biệt C, D (C nằm giữa M và D). Gọi N  là giao điểm của AB và CD.

a) Chứng minh rằng tứ giác OAMB nội tiếp.

b) Chứng minh rằng \(\Delta ANC\) và \(\Delta DNB\) đồng dạng, \(\Delta AMC\) và \(\Delta DMA\) đồng dạng.

c) Chứng minh rằng:\(\dfrac{{MC}}{{MD}} = \dfrac{{NC}}{{ND}}.\)

d) Xác định vị trí của đường thẳng \(\left( d \right)\) để \(\dfrac{1}{{MD}} + \dfrac{1}{{ND}}\) đạt giá trị nhỏ nhất.

Câu 4

Cho \(a,\;b\) là các số thực không âm thỏa mãn \({a^{2018}} + {b^{2018}} = {a^{2020}} + {b^{2020}}.\) Tìm giá trị lớn nhất của biểu thức \(P = {\left( {a + 1} \right)^2} + {\left( {b + 1} \right)^2}.\)

Câu 1 :

a) Bằng các phép biến đổi đại số hãy rút gọn biểu thức: \(A = 2\sqrt 5  + 3\sqrt {45} .\)

b) Giải phương trình \({x^2} - 6x + 5 = 0.\) 

Câu 2 :

Cho hai hàm số \(y = {x^2}\) và \(y =  - x + 2.\)

a) Vẽ đồ thị của hai hàm số này trên cùng một mặt phẳng tọa độ Oxy.

b)  Tìm tọa độ giao điểm của hai đồ thị đó bằng phương pháp đại số.

Câu 3 :

Cho phương trình \({x^2} - 2x + m + 3 = 0\;\;\;\left( 1 \right)\) (với \(x\) là ẩn, \(m\) là tham số).

a) Tìm tất cả các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có nghiệm.

b) Gọi \({x_1},\;{x_2}\) là nghiệm của phương trình \(\left( 1 \right).\) Tìm tất cả các giá trị của \(m\) để \(x_1^2 + x_2^2 - 3{x_1}{x_2} - 4 = 0.\)

Câu 4 :

Một mảnh đất hình chữ nhật có diện tích \(360{m^2}.\) Nếu tăng chiều rộng \(2m\) và giảm chiều dài \(6m\) thì diện tích mảnh đất không đổi. Tính chu vi của mảnh đất lúc đầu.

Câu 5 :

Cho đường tròn \(\left( O \right)\) đường kính \(AB = 6cm.\) Gọi \(H\) là điểm thuộc đoạn thẳng \(AB\) sao cho \(AH = 1cm.\)  Qua  \(H\) vẽ đường thẳng vuông góc với \(AB,\)  đường thẳng này cắt đường tròn \(\left( O \right)\) tại C và D. Hai đường thẳng BC và AD cắt nhau tại M. Gọi N là hình chiếu của M trên đường thẳng AB.

a) Chứng minh tứ giác MNAC nội tiếp.

b) Tính độ dài CH và \(\tan \angle ABC\)

c) Chứng minh NC là tiếp tuyến của đường tròn \(\left( O \right)\).

d) Tiếp tuyến tại A của đường tròn \(\left( O \right)\) cắt NC tại E. Chứng minh đường thẳng EB đi qua trung điểm của đoan thẳng CH.

Bài 1  Các đẳng thức sau đúng hay sai, giải thích?

a) \(\sqrt {{{\left( { - 3} \right)}^2}}  =  - 3.\)   

b) \(\dfrac{{x - y}}{{\sqrt x  + \sqrt y }} = \sqrt x  - \sqrt y \)  với \(x > 0,\;\;y > 0.\)

Bài 2  Giải phương trình và hệ phương trình sau:

\(a)\;\;2{x^2} - 5x + 2 = 0.\)

\(b)\;\left\{ \begin{array}{l}2x + y = 1\\3x - 2y = 5\end{array} \right..\)

Bài 3 

Cho hai hàm số \(\left( P \right):\;\;y = {x^2}\) và \(d:\;\;y = x + 2m + 10,\) với \(m\) là tham số.

a) Vẽ đồ thị \(\left( P \right)\) trên hệ trục tọa độ \(Oxy.\)

b) Tìm giá trị của tham số \(m\) biết \(d\) cắt \(\left( P \right)\) tại điểm có hoành độ bằng \(5.\)

Bài 4 

Đua ghe ngo là một trong những nét văn hóa truyền thống độc đáo của đồng bào dân tộc Khmer Nam Bộ. Cuộc đua luôn thu hút hàng trăm ngàn người tham dự vào dịp lễ hội Ok-om-bok hàng năm (rằm tháng 10 âm lịch). Đua ghe ngo là dịp để các đội ghe đến tham gia tranh tài, qua đó nhằm tôn vinh, nâng cao ý thức bảo tồn di sản văn hóa truyền thống của địa phương, thể hiện tinh thần đoàn kết dân tộc, khơi dậy niềm tự hào, tinh thần yêu quê hương đất nước

Tại lễ hội đua ghe ngo Sóc Trăng, có 56 đội ghe trong và ngoài đăng ký tham gia. Lúc đầu ban tổ chức dự kiến chia 56 đội thành các bảng đấu với số đội ở mỗi bảng bằng nhau. Tuy nhiên, đến ngày bốc thăm chia bảng thì có 1 đội không tham dự được, vì vậy ban tổ chức quyết định tăng ở mỗi bảng thêm 1 đội, do đó tổng số bảng đấu giảm đi 3 bảng. Hỏi số bảng đấu dự kiến lúc đầu là bao nhiêu?

Bài 5  Cho tam giác \(ABC\) có ba góc nhọn, nội tiếp đường tròn \(\left( O \right),\;\;AB > AC\) và  các đường cao \(AD,\;\;BE,\;\;CF\) cắt nhau tại \(H.\)

a) Gọi \(I\) là trung điểm của \(AH,\) chứng minh \(AEHF\) nội tiếp đường tròn \(\left( I \right).\)

b) Chứng minh \(DB.DC = DA.DH.\)

c) Gọi \(K\) là giao điểm khác \(A\) của hai đường tròn \(\left( O \right)\) và \(\left( I \right).\) Chứng minh \(OI//HK.\)

Câu 1 

a) Tìm \(x\) để biểu thức sau có nghĩa: \(P = \sqrt {5x + 3}  + 2018\sqrt[3]{x}.\)

b) Cho hàm số \(y = \dfrac{1}{2}{x^2}.\) Điểm \(D\) có hoành độ \(x =  - 2\) thuộc đồ thị hàm số. Tìm tọa độ điểm \(D.\)

c) Tìm giá trị của \(a\) và \(b\) để đường thẳng \(d:\;\;y = ax + b - 1\) đi qua hai điểm \(A\left( {1;\;1} \right)\) và \(B\left( {2;\;3} \right).\)

Câu 2 

Cho biểu thức: \(P = \dfrac{{x\sqrt y  + y\sqrt x }}{{\sqrt {xy} }} - \dfrac{{{{\left( {\sqrt x  + \sqrt y } \right)}^2} - 4\sqrt {xy} }}{{\sqrt x  - \sqrt y }} - y\) (với \(x > 0,\;\;y > 0,\;\;x \ne y\)).

a) Rút gọn biểu thức \(P.\)               

b) Chứng minh rằng \(P \le 1.\)

Câu 3 

Cho phương trình \({x^2} - 4mx + 4{m^2} - 2 = 0\;\;\;\left( 1 \right)\)

a) Giải phương trình \(\left( 1 \right)\) khi \(m = 1.\)

b) Chứng minh rằng với mọi \(m\) phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt.

Giả sử hai nghiệm là \({x_1},\;{x_2}\) khi đó tìm \(m\) để \(x_1^2 + 4m{x_2} + 4{m^2} - 6 = 0.\)

Câu 4 

Cho hình chữ nhật ABCD nội tiếp đường tròn tâm O. Tiếp tuyến của đường tròn tâm O tại điểm C cắt các đường thẳng AB và AD  theo thứ tự tại M, N. Dựng AH  vuông góc với BD tại điểm H,  K  là giao điểm của hai đường thẳng MN  và BD.

a) Chứng minh tứ giác AHCK là tứ giác nội tiếp.

b) Chứng minh AD.AN = AB.AM.

c) Gọi E  là trung điểm của MN. Chứng minh ba điểm A, H, E thẳng hàng.

d) Cho AB = 6cm, AD = 8cm. Tính độ dài đoạn MN.

Câu 5 : Giải phương trình: \(3\sqrt 3 \left( {{x^2} + 4x + 2} \right) - \sqrt {x + 8}  = 0.\)

Câu 1 : Không dùng máy tính cầm tay, hãy giải phương trình: \(\left( {x - 2018} \right)\left( {x - 2020} \right) = 2018 - x.\)

Câu 2 : Không dùng máy tính cầm tay, tính giá trị biểu thức: \(A = \dfrac{{\sqrt {15}  - \sqrt {12} }}{{\sqrt 5  - 2}} - \dfrac{1}{{2 - \sqrt 3 }}.\)

Câu 3 : Rút gọn biểu thức: \(P = \left( {\dfrac{{3\sqrt x }}{{\sqrt x  + 2}} + \dfrac{{\sqrt x }}{{\sqrt x  - 2}} - \dfrac{{x - \sqrt x }}{{x - 4}}} \right):\dfrac{{3\sqrt x }}{{\sqrt x  + 2}}\)  với \(x > 0,\;\;x \ne 4.\) 

Câu 4 : Cho hàm số bậc nhất \(y = mx + 1\) với \(m\) là tham số. Tìm \(m\) để đồ thị hàm số đi qua điểm \(A\left( {1;\;4} \right).\)  Với giá trị \(m\) vừa tìm được, hàm số đồng biến hay nghịch biến trên \(R.\)

Câu 5 : Giải hệ phương trình: \(\left\{ \begin{array}{l}3\left( {x + 1} \right) + 2\left( {x + 2y} \right) = 4\\4\left( {x + 1} \right) - \left( {x + 2y} \right) = 9\end{array} \right..\)

Câu 6 : Cho phương trình \({x^2} - 4x + 4m - 3 = 0\) với \(m\) là tham số. Tìm giá trị của \(m\) để phương trình có hai nghiệm \({x_1};\;{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 14.\)

Câu 7 : Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH,\) biết \(AC = 16cm\) và \(\sin \widehat {CAH} = \dfrac{4}{5}.\) Tính độ dài các cạnh \(BC,\;AB.\)

Câu 8: Cho hai đường tròn \(\left( {O;\;4cm} \right)\) và \(\left( {O';\;11cm} \right).\) Biết khoảng cách \(OO' = 2a + 3\;\left( {cm} \right)\) với \(a\) là số thực dương. Tìm \(a\) để hai đường tròn tiếp xúc nhau.

Câu 9 : Cho đường tròn tâm O, dây cung AB không đi qua tâm O. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây cung MC không đi qua tâm O cắt đoạn thẳng AB tại D (D khác A, D khác B). Đường thẳng vuông góc với AB tại D, cắt OC tại K.Chứng minh rằng tam giác KCD là tam giác đều.

Câu 10 : Cho tam giác ABC có ba góc nhọn và AB < AC nội tiếp đường tròn tâm O. Các đường cao BE, CF của tam giác ABC cắt nhau tại H.

a) Chứng minh tứ giác AFHE nội tiếp được trong một đường tròn. Xác định tâm và bán kính của đường tròn đó.

b) Gọi M là giao điểm của EF và BC, đường thẳng MA cắt (O) tại điểm thứ hai là I khác A. Chứng minh tứ giác AEFI nội tiếp được một đường tròn.

Câu 1 

1) Tính giá trị của biểu thức: \(A = \sqrt {4 - 2\sqrt 3 }  - \dfrac{1}{2}\sqrt {12} .\)

2) Giải phương trình và hệ phương trình sau:

\(a)\;{x^4} + {x^2} - 20 = 0\)   

\(b)\;\left\{ \begin{array}{l}3x - y = 11\\2x + y = 9\end{array} \right..\)  

3) Cho phương trình \({x^2} - 2x - 5 = 0\) có hai nghiệm \({x_1},\;{x_2}.\) Không giải phương trình, hãy tính giá trị của các biểu thức: \(B = x_1^2 + x_2^2,\;\;C = x_1^5 + x_2^5.\)

Câu 2 : Trong mặt phẳng tọa độ \(Oxy\) cho parabol \(\left( P \right):\;\;y = \dfrac{1}{2}{x^2}\) và đường thẳng \(\left( d \right):\;\;y = x + m.\)

1) Vẽ \(\left( P \right)\) và \(\left( d \right)\) trên cùng một hệ trục tọa độ khi \(m = 2.\)

2) Định các giá trị của \(m\) để \(\left( d \right)\)cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\) và \(B.\)

3) Tìm giác trị của \(m\) để độ dài đoạn thẳng \(AB = 6\sqrt 2 .\)

Câu 3 : Hai bến sông A và B cách nhau 60km. Một ca nô đi xuôi dòng từ A đến B rồi ngược dòng về A. Thời gian đi xuôi dòng ít hơn thời gian đi ngược dòng là 20 phút. Tính vận tốc ngược dòng của ca nô, biết vận tốc xuôi dòng lớn hơn vận tốc ngược dòng của ca nô là 6 km/h.

Câu 4 : Cho tam giác ABC có ba góc nhọn (AB < AC), các đường cao AF, BD và CE cắt nhau tại H.

1) Chứng minh tứ giác BEDC nội tiếp đường tròn.

2) Chứng minh AE.AB = AD.AC.

3) Chứng minh FH  là phân giác của \(\widehat {EFD}.\)

4) Gọi O là trung điểm của đoạn thẳng BC. Chứng minh \(\widehat {DOC} = \widehat {FED}.\)  

Câu 5 : Một hình trụ có diện tích xung quanh bằng \(256\pi c{m^2}\) và bán kính đáy bằng \(\dfrac{1}{2}\) đường cao. Tính bán kính đáy và thể tích hình trụ.

Câu I: 

1) Giải phương trình: \({x^2} + 8x + 7 = 0\)

2) Giải hệ phương trình: \(\left\{ \begin{array}{l}2x - y =  - 6\\5x + y = 20\end{array} \right.\)

Câu II: 

Cho biểu thức \(A = \dfrac{{\sqrt x  + 1}}{{x + 4\sqrt x  + 4}}:\left( {\dfrac{x}{{x + 2\sqrt x }} + \dfrac{x}{{\sqrt x  + 2}}} \right),\) với \(x > 0\)

1. Rút gọn biểu thức A.

2. Tìm tất cả các giá trị của x để \(A \ge \dfrac{1}{{3\sqrt x }}\)

Câu III: 

1. Cho đường thẳng \(\left( d \right):\,\,y = ax + b\) . Tìm \(a,b\) để đường thẳng (d) song song với đường thẳng \(\left( {d'} \right):\,\,y = 2x + 3\) và đi qua điểm \(A\left( {1; - 1} \right)\)

2. Cho phương trình \({x^2} - \left( {m - 2} \right)x - 3 = 0\) (m là tham số). Chứng minh phương trình luôn có hai nghiệm phân biệt \({x_1};{x_2}\)  với mọi m. Tìm m để các nghiệm đó thỏa mãn hệ thức:

\(\sqrt {x_1^2 + 2018}  - {x_1} = \sqrt {x_2^2 + 2018}  + {x_2}\)

Bài IV: 

Cho đường tròn tâm \(\left( O \right)\), đường kính \(AB = 2R\). Gọi \({d_1};{d_2}\) lần lượt là các tiếp tuyến của đường tròn \(\left( O \right)\) tại A và B, I là trung điểm của đoạn thẳng OA, E là điểm thay đổi trên đường tròn \(\left( O \right)\) sao cho E không trùng với A và B. Đường thẳng d đi qua E và vuông góc với đường thẳng EI cắt \({d_1};{d_2}\) lần lượt tại M, N.

1. Chứng minh AMEI là tứ giác nội tiếp.

2. Chứng minh \(IB.NE = 3IE.NB\)

3. Khi điểm E thay đổi, chứng minh tích \(AM.BN\) có giá trị không đổi và tìm giá trị nhỏ nhất của diện tích tam giác MNI theo R.

Câu V: 

Cho \(a,b,c\) là các số thực dương thỏa mãn: \(a + b + c = 1\) . Chứng minh \(\dfrac{1}{{{a^2} + {b^2} + {c^2}}} + \dfrac{1}{{abc}} \ge 30.\)

Bài 1 :

a) Tính giá trị biểu thức: \(A = 3\sqrt {27}  - 2\sqrt {12}  + 4\sqrt {48} .\)        

b) Rút gọn biểu thức: \(B = \sqrt {7 - 4\sqrt 3 }  + \dfrac{1}{{2 - \sqrt 3 }}.\)

Bài 2 : Giải các phương trình và hệ phương trình sau:

a) \({x^2} - 3x + 2 = 0\)                     

b) \({x^2} - 2\sqrt 3 x + 3 = 0\)

c) \({x^4} - 9{x^2} = 0\)                       

d) \(\left\{ \begin{array}{l}x - y = 3\\3x - 2y = 8\end{array} \right.\)

Bài 3:

a)  Trong mặt phẳng tọa độ Oxy, cho Parabol (P): \(y = {x^2}\) . Vẽ đồ thị Parabol  (P).

b)  Cho phương trình: \({x^2} - \left( {m - 1} \right)x - m = 0\,\,\,\left( 1 \right)\)  ( với x là ẩn số, m là tham số). Xác định các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1};{x_2}\)  thỏa mãn điều kiện:  \({x_1}\left( {3 - {x_2}} \right) + 20 \ge 3\left( {3 - {x_2}} \right)\)

Bài 4 :

Quãng đường AB dài 160 km. Hai xe khởi hành cùng một lúc từ A để đi đến B. Vận tốc của xe thứ nhất lớn hơn vận tốc của xe thứ hai là 10 km/h nên xe thứ nhất đến B sớm hơn xe thứ hai là 48 phút. Tính vận tốc của xe thứ hai.

Bài 5 :

Cho tam giác ABC vuông tại A, đường cao AH. Gọi M là trung điểm của BC. Biết AB = 3 cm, AC = 4cm. Tính độ dài đường cao AH và diện tích tam giác ABM.

Bài 6 :

Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O; R). Các đường cao AD, BE, CF của tam giác ABC cắt nhau tại H. Gọi M là trung điểm của BC.

a) Chứng minh tứ giác BFHD nội tiếp được đường tròn.

b) Biết \(\widehat {EBC} = {30^0}.\) Tính số đo \(\widehat {EMC}\) .

c) Chứng minh \(\widehat {FDE} = \widehat {FME}\)

Bài 7 :    Cho \(a = \dfrac{{\sqrt 2  - 1}}{2};b = \dfrac{{\sqrt 2  + 1}}{2}.\) Tính \({a^7} + {b^7}\)

PHẦN I: TRẮC NGHIỆM

Câu 1: Cho biểu thức \(P = a\sqrt 2 \) với \(a < 0.\) Khi đó biểu thức P bằng

A. \(\sqrt { - 2a} \)         

B. \( - \sqrt { - 2a} \)               

C. \(\sqrt {2{a^2}} \)        

D. \( - \sqrt {2{a^2}} \)

Câu 2: Hàm số \(y = \left( {m - 4} \right)x + 7\) đồng biến trên \(R,\) với:

A. \(m \ge 4\)             

B. \(m > 4\)           

C. \(m < 4\)           

D.\(m \ne 4\)

Câu 3: Số nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\3x + 2y = 4\end{array} \right.\)  là:

A. 1                             B. 2     

C. vô số                       D. 0

Câu 4: Cho hình chữ nhật \(ABCD\) có \(AB = 2\sqrt 3 \;cm,\;\;BC = 2\;cm.\) Độ dài đường kính của đường tròn ngoại tiếp hình chữ nhật \(ABCD\) bằng:

A. \(2\;cm\)           

B. \(2\sqrt 3 \;cm\)         

C. \(4\;cm\)     

D. \(8\;cm\)

II. TỰ LUẬN 

Câu 5 . Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3 = 0\,\,\left( 1 \right),\) với m là tham số và x là ẩn số.

a)  Giải phương trình (1) khi m = 3.

b)  Tìm tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt.

Câu 6 

a) Trên mặt phẳng Oxy, cho parabol \(\left( P \right):\,\,y = \dfrac{1}{4}{x^2}\) và A, B là 2 điểm thuộc (P) có hoành độ tương ứng bằng \( - 2\)  và 4. Tìm tọa độ hai điểm A, B và viết phương trình đường thẳng d đi qua hai điểm A, B.

b) Cho một mảnh vườn hình chữ nhật. Biết rằng nếu giảm chiều rộng đi 3m và tăng chiều dài thêm 8m thì diện tích mảnh vườn đó giảm đi \(54{m^2}\) so với diện tích ban đầu, nếu tăng chiều rộng thêm 2m và giảm chiều dài đi 4m thì diện tích mảnh vườn đó tăng \(32{m^2}\)  so với diện tích ban đầu. Tính chiều rộng và chiều dài ban đầu của mảnh vườn đó?

Câu 7 . Cho đường tròn (O;R) ( đường tròn tâm O, bán kính R) và điểm A cố định nằm trên đường tròn (O;R). BC là một đường kính thay đổi của đường tròn (O;R) và không đi qua điểm A. Đường tròn đường kính AO cắt các đoạn AB, AC tại các điểm thứ hai tương ứng là M, N. Tia OM cắt (O;R) tại điểm P. Gọi H là trực tâm của tam giác AOP. Chứng minh rằng:

a) Tứ giác AMON là hình chữ nhật.

b) Tứ giác PHOB nội tiếp được trong một đường tròn và \(\dfrac{{OH.PC}}{{AC}}\) không phụ thuộc vị trí của các điểm B, C.

c) Xác định vị trí của các điểm B, C sao cho tam giác AMN có diện tích lớn nhất.

Câu 8 . Giải phương trình : \(\sqrt {2\left( {{x^4} + 4} \right)}  = 3{x^2} - 10x + 6\)

Bài 1 :

a)  Giải phương trình \({x^2} + 4x - 5 = 0.\)

b)  Giải hệ phương trình \(\left\{ \begin{array}{l}x - y = 1\\2x + y = 5\end{array} \right.\)

c)  Rút gọn biểu thức \(P = \sqrt {16}  - \sqrt[3]{8} + \frac{{\sqrt {12} }}{{\sqrt 3 }}.\)

Bài 2 : Cho parabol \(\left( P \right):\;\;y = 2{x^2}\) và đường thẳng \(\left( d \right):\;\;y = 2x + m\) (m là tham số).

a) Vẽ parabol \(\left( P \right).\)

b) Với những giá trị nào của \(m\) thì \(\left( P \right)\) và \(\left( d \right)\) chỉ có một điểm chung. Tìm tọa độ điểm chung đó.

Bài 3 :

a) Hai ô tô khởi hành cùng một lúc từ thành phố A đến thành phố B cách nhau 450 km với vận tốc không đổi. Vận tốc xe thứ nhất hơn vận tốc xe thứ hai 10 km/h nên xe thứ nhất đến thành phố B trước xe thứ hai 1,5 giờ. Tính vận tốc mỗi xe.

b) Cho phương trình: \({x^2} - mx - 1 = 0\) (m là tham số). Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\;\;{x_2}\) thỏa mãn \({x_1} < {x_2}\) và \(\left| {{x_1}} \right| - \left| {{x_2}} \right| = 6.\)

Bài 4 : Cho đường tròn (O;R) và điểm A ở bên ngoài đường tròn đó.  Kẻ cát tuyến  AMN không đi qua O (M nằm giữa A và N). Kẻ hai tiếp tuyến AB, AC với (O;R) (B, C là hai tiếp điểm và C thuộc cung nhỏ MN). Đường thẳng BC cắt MN và AO lần lượt tại E, F. Gọi I là trung điểm của MN.

a)  Chứng minh tứ giác ABOC nội tiếp được trong đường tròn.

b)  Chứng minh \(EB.EC = EM.EN\) và IA là tia phân giác của góc \(\widehat {BIC}.\)

c)  Tia MF cắt (O;R) tại điểm thứ hai là D. Chứng minh \(\Delta AMF \sim \Delta AON\)  và  \(BC\parallel DN.\)

d)  Giả sử AO = 2R. Tính diện tích tam giác ABC theo R.

Bài 5 :

a) Giải phương trình: \(2\sqrt x  - \sqrt {3x + 1}  = x - 1.\)

b) Cho hai số thực dương \(a,\;b\) thỏa mãn \(a + b + 3ab = 1.\) Tìm giá trị lớn nhất của biểu thức \(P = \sqrt {1 - {a^2}}  + \sqrt {1 - {b^2}}  + \frac{{3ab}}{{a + b}}.\)